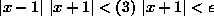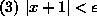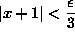какого-то очевидного свойства абсолютной величины.
может такого:
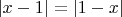

только не поможет. умножая на -1 переводим направление неравенства, но перейдти на модуль не получится.
-- 24.04.2015, 22:52 --но не могу строго перейти от

к

американцы это делают здесь
Там не это написано. Лучше перепишите сюда внимательней. И лучше полнее, иначе утрачивается всякий смысл.
что вы имеете в виду ? обьясните пожалуйста.
там написано так (полнее):
We will now ``replace" the term |x-1| with an appropriate constant and keep the term |x+1| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that
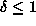
(This is a valid assumption to make since, in general, once we find a
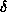
that works, all smaller values of
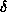
also work.). Then
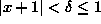
implies that -1 < x+1 < 1 and -2 < x < 0 so that 1 < |x-1| < 3 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and tex2html_wrap_inline574. This guarantees the logic of the proof.)