У нузимата есть 100 одинаковых по внешнему виду монет. Он знает, что стреди них 30 настоящих и 70 фальшивых. Кроме того, он знает, что массы всех настоящих монет одинаковы, а массы всех фальшивых монет -- разные, причем каждая фальшивая монета тяжелее настоящей, однако точные массы монет неизвестны.
Имеются двухчашечные весы без гирь, на которых можно за одно взвешивание сравнить массы двух групп, состоящих из одинакового количества монет.
За какое наименьшее количество взвешиваний на этих весах, нузимат может гарантированно найти хотя бы одну настоящую монету?
Самая легкая -- настоящая монета. Заглавные буквы -- название кучек, прописные -- количество монет в них.
Разбиваем на две кучки

и

по 50 монет.
1) Взвешиваем, для определенности будет результат

.
Значит в кучке

будет

монет настоящих.
2) Взвешиваем по 25 монет из кучки

, получаем разбиение на

и

.
Для определенности

, тогда в кучке

будет

настоящих монет.
3) Рассматриваем кучку

, разбиваем ее на две кучки

и

по 12 монет в каждой, + еще одна отложенная монета.
Для определенности

, тогда в кучке

будет

настоящие монеты.
4) Кучку

разбиваем на

и

по шесть монет в каждой, для определенности

, тогда в кучке

будет

[/math] настоящих.
5) Кучку

разбиваем на

и

по три монеты в каждой, для определенности

, тогда в кучке

будет
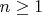
[/math] настоящая.
6) Берем кучку

из трех монет. Выбираем две из них, взвешиваем. Если будет равенство, то это настоящие. Если одна будет легче, то она настоящая.
То есть 6 взвешиваний. Но как доказать, что число 6 нельзя уменьшить? Верно ли проведены рассуждения?