Я не захотел останавливаться и поэтому решил вывести формулу магнитной индукции для конечного проводника.
Пусть есть проводник длиной

. Нужно найти модуль магнитной индукции в точке

, находящейся на расстоянии

от проводника и на одинаковых расстояниях от концов проводника.
Тогда, как уже ранее было выяснено,

Теперь надо определить пределы интегрирования. Я рискнул и предположил следующее:

- это расстояние от элемента тока

до проекции точки

на провод. Это расстояние пробегает все значения от

до

(снизу вверх) и потом ещё от

до

(тоже снизу вверх).
Получается,

Теперь надо проверить правильность полученного результата. Должно выполняться следующее:

. Всё хорошо выполняется, значит я получил правильный ответ.
Но потом я подумал вот о чём.

зависит от

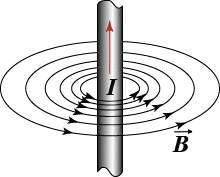
. Почему так происходит? Ведь вокруг проводника создаётся магнитное поле, линии индукции которого являются окружностями, перпендикулярными самому проводу. Тогда, если провести плоскость через точку

, перпендикулярно проводу, то получится, что только "часть провода действует на точку". Весь остальной провод создаёт поле, которое никак не может попасть в точку

. Почему же тогда индукция в точке зависит от длины провода?