Кажется разобрался. Если и тут накосячил - посыпаю голову пеплом и закапываюсь в справочники.
Моя основная ошибка - я считал величины

,

и
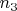
неслучайными из-за того, что нам известна

. Пример с кубиком - поразительно универсальная вещь

То есть, условие "имеем выборку из

элементов" интерпретировал, как "имеем выборку из

элементов, причем

выпал

раз,

-

раз и

-
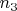
раз". Собственно, на этом моменте рассуждения и клинились.
Дальше, по поводу мат. ожидания. Тут самое слабое место рассуждений - некоторые определения просто не хотят откладываться в голове, пытаюсь восполнять изучением примеров.
Итак, абстрагируясь от километровых рассуждений, мат. ожидание у нас - некое среднее, которое мы ожидаем увидеть.
Исходя из вероятностей, представленных в условии, мы ожидаем увидеть

элементов

,

элементов

и (самое главное для нас)

элементов

. Суммируем для проверки вышеуказанные величины, получаем

.
Таким образом, мат. ожидание
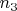
будет равно

.
Тут же, пока мысль не потерялась, использую совет с заменой

и нахожу

.

Отсюда очень своевременно выходит, что оценка несмещенная (условие необходимое, а было проигнорировано в первых выкладках).
Собственно, дальше

будет вычисляться, как

и подставляться в "заготовку" из прошлых постов под Рао-Крамера. Пока, правда, выскакивает проблема с мат. ожиданием

(именно параметра исходного), но тут уже, насколько понимаю, пойдёт возня со скобками и выражением одних величин через другие. Тем более, что сам

может принимать только определенные значения и они легко вычисляются.