Модель Солоу

[jizu]

Добрый вечер!
Решая задание, столкнулся с проблемой нахождения точки перегиба.
Посмотрите, пожалуйста, ошибки.
Зеленым выделил то, что не получается найти (система не принимает числа)
Помогите найти решение

Задание:
Расчёт параметров в односекторной модели экономического роста
Производственная функция имеет вид:
$X=0.6K^ \frac2 3 \cdot L^ \frac1 3$

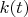
$A=0.6; \alpha= \frac2 3$ параметры производственной функции; доля выбывших за год основных производственных фондов $\mu=0.07$; годовой темп прироста численности занятых в производстве $\nu=0.03; k_0$начальное значение функции фондовооруженности $k(t)$, принимает три различных значения: 15,3,87.

Постановка задачи.
1. Составить модель экономического роста в удельных показателях в виде дифференциального уравнения.
2. Найти его решение при заданных условиях.
3. Построения графика интегральных кривых. Сделать выводы.

Алгоритм выполнения задачи:
1. Найти значение $p= \tilde{p}$ , при котором функция $g(p)=(1-p)^{1- \alpha} \cdot p^{ \alpha }$, определяющая наибольшее возможное значение среднедушевого потребления, достигает максимума. Для этого:
Заданное α подставить в функцию $g(p)$, продифференцировать по p и исследовать знаки производной;
Если происходит смена знака в критической точке, тогда функция имеет экстремум.
2. Составить модель экономического роста для заданных параметров $А$ и $\alpha$ производственной функции Кобба-Дугласа, производственных показателей $ \nu , \mu $ и найденного оптимального значения нормы накопления $p$.
3. Из уравнения $-(\mu+\nu)k+A \cdot \tilde{p}k^ \alpha $ определить равновесный уровень фондовооруженности $k$.
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными.
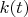
5. Найти зависимость $k(t)$ от начального значения $k_0$.
6. Провести исследование и построить интегральные кривые $k_1 (t), k_2 (t), k_3 (t)$ для заданных в таблице начальных значений $k_0$; описать типы переходных режимов.

Решение:
1. Найдем оптимальное значение нормы накопления $p=\tilde{p}$ при котором функция среднедушевого потребления достигает максимума.
1а. Функция, от которой зависит оптимальное значение среднедушевого потребления, имеет вид:

$$g(p)=(1-p)^{ \frac1 3} \cdot p^{ \frac2 3}$$

1б. Производственная функции $g(p)$ имеет вид:

$$\frac{dg}{dp}=(\frac{p}{1-p})^\frac1 3 \cdot (\frac {\frac2 3-p}{p}) \Rightarrow p=\frac2 3$$

$$\frac{dk}{dt}= -(\mu+\nu)k+A \cdot \tilde{p}k^ \alpha $$

$$\frac{dk}{dt}= -(0.07+0.03)k=0.67 \cdot 0.6k^\frac2 3$$

2. Дифференциальное уравнение, определяющее уровень фондовооруженности имеет вид:

$$\frac{dk}{dt}=-0.1k+0.4k^\frac2 3$$

3. Определим уровень фондовооруженности $k^*$ при условии $\frac{dk}{dt}=0$
$k^*$ стационарный режим (т.е. не зависящий от времени $t$)

$$-0.1k+0.4k^\frac2 3=0$$

$$k-4k^\frac2 3=0$$

4. Решим дифференциальное уравнение с разделяющимися переменными:

$$\frac{dk}{dt}=-0.1k+0.4k^\frac2 3$$

4а. Интеграл в левой части равенства имеет вид:

$$k=u^\frac1 2=u^\frac3 2;dk=1.5udu$$

$$-\int\limits_{}^{} \frac{15 \cdot u^\frac 1 2} {u^\frac3{ 2} -4u} du$$

4б. Сократим на $u$, применяя метод подведения под знак дифференциала, обозначив через $s$ знаменатель дроби

$$[u-4=s; du=ds]$$

$$-30\int\limits_{}^{} \frac {ds} s$$

$$-30 \ln|S|=t+C$$

$$\ln|S|=-0.03t+C$$

$$\ln|S|=\ln e^{-0.03t} \cdot C$$

$$\sqrt[3]{k}-4=Ce^{-0.03t} $$

$$\sqrt[3]{k}=Ce^{-0.03t}+4$$

4в. Общее решение дифференциального уравнения имеет вид:

$$k(t)=[4+\tilde{C}e^{-0.03t}]^3$$

$$\sqrt[3]{k_0}=4+\tilde{C}e^{-0.03 \cdot 0}$$

$$ \tilde{C}= \sqrt[3]{k_0}-4 \Rightarrow \tilde{C}= k_0^ \frac{1} {3} -4 $$

5. Интегральные кривые имеют вид:

$$k_1 (t)=[4+(\sqrt[3]{15}-4) e^{-0.03t} ]^3$$

$$k_2 (t)=[4+(\sqrt[3]{3}-4) e^{-0.03t} ]^3$$

$$k_3 (t)=[4+(\sqrt[3]{87}-4) e^{-0.03t} ]^3$$

$$k_1 (t)=[4-1.53 \cdot e^{-0.03t} ]^3$$

$$k_2 (t)=[4-2.56 \cdot e^{-0.03t} ]^3$$

$$k_3 (t)=[4+0.43 \cdot e^{-0.03t} ]^3$$

6. Возрастание и убывание функций:
$k_1 (t)$-возрастает
$k_2 (t)$-возрастает
$k_3 (t)$-убывает
7. Найдем знаки и критические точки $k'' (t)$. А также укажем значение $\hat{k}$для определения точки перегиба.

$$k'' (t)=(-0.1k+0.4\sqrt[3]{k})' \cdot k' (t)=(-0.1+0.4 \cdot \frac1 3 (k)^\frac{-2} {3}) \cdot k' (t)$$

8. Значение $\hat{k}$ для определения точек перегиба.
$\hat{k}=$

[iifat]

(Оффтоп)

(голосом честной девушки при виде презерватива) Ворд?!

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[jizu]

никто не знает что ли?

[Deggial]

jizu в сообщении #1009542 писал(а):

никто не знает что ли?

jizu, замечание за подъём темы бессодержательным сообщением.

[svv]

jizu
Вы можете более кратко сформулировать вопросы, чтоб не приходилось всё читать? Типа «как решить такое-то уравнение?», или «как найти такую-то величину, если известно то и это?».

[ShiNeko]

Цитата:

3. Определим уровень фондовооруженности $k^*$ при условии $\frac{dk}{dt}=0$
$k^*$ стационарный режим (т.е. не зависящий от времени $t$)

$$-0.1k+0.4k^\frac2 3=0$$

$$k-4k^\frac2 3=0$$

Я не могу понять в чем проблема? Нашли отсюда $k=64.$ Число не устраивает?

Цитата:

7. Найдем знаки и критические точки $k'' (t)$. А также укажем значение $\hat{k}$для определения точки перегиба.

$$k'' (t)=(-0.1k+0.4\sqrt[3]{k})' \cdot k' (t)=(-0.1+0.4 \cdot \frac1 3 (k)^\frac{-2} {3}) \cdot k' (t)$$

8. Значение $\hat{k}$ для определения точек перегиба.
$\hat{k}=$

Здесь ошибка, должно быть
$k'' (t)=(-0.1k+0.4k^{\frac{2}{3}})' \cdot k' (t)=(-0.1+0.4 \cdot \frac{2} {3}k^{-\frac{1} {3}}) \cdot k' (t),$ если Вы нашли правильно k'(t)

[jizu]

svv в сообщении #1009690 писал(а):

jizu
Вы можете более кратко сформулировать вопросы, чтоб не приходилось всё читать? Типа «как решить такое-то уравнение?», или «как найти такую-то величину, если известно то и это?».

Я расписал своё решение, чтобы если уж ошибка, найти её
И указал, что зеленый цвет не получается сделать.

Цитата:

Здесь ошибка, должно быть
$k'' (t)=(-0.1k+0.4k^{\frac{2}{3}})' \cdot k' (t)=(-0.1+0.4 \cdot \frac{2} {3}k^{-\frac{1} {3}}) \cdot k' (t),$ если Вы нашли правильно k'(t)

Только вот, найденное число онлайн система не берет.
Не могу сказать,правильно или нет. Система приняла всё до этого момента. Дальше как не понимаю
Я уже все числа перебрал. Не знаю, каким образом сдать задание для курсовой
Преподаватель толком помочь не может

Вот: http://cfile.ru/ab/img/png%20%2881%29.png

[Otta]

jizu

ShiNeko в сообщении #1009704 писал(а):

Найдем знаки и критические точки $k'' (t)$. А также укажем значение $\hat{k}$ для определения точки перегиба.

И что это означает? Я еще могу понять, если нужно указать значение $\hat{k}$ точки перегиба, но какое-то значение для ее определения - это как?

Ищите вторую производную до конца, раз это от Вас все равно требуется, и выясните, что же такое $\hat{k}$.

[jizu]

Закрывайте тему, ибо ничего не понятно