Здравствуйте. Прошу помочь разобраться в решение задачи. Преподаватель сказал, что не правильно.
Сферический слой из диэлектрика с относительной проницаемостью

имеет внутренний радиус

cм и внешний радиус

см. По слою распределён заряд, объёмная плотность которого убывает от внутренней поверхности слоя к внешней по закону

, где

Кл/

Найти разность потенциалов
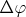
между внутренней и внешней поверхностями слоя.
Решение

Рассмотрим сферический слой радиуса

и малой толщины

Разность потенциалов между внутренний и внешней поверхностями этого слоя:

где

напряженность поля создаваемого сферическим слоем с внешним радиусом

и внутренним радиусом

у внешней поверхности этого слоя.

заряд этого слоя.

объем сферического слоя радиусом

и толщиной



но преподаватель сказал, что этот интеграл не правильный. Почему?
Могу выложить решение целиком, но не вижу смысла т.к ошибка в этом интеграле.