Нахождение площади фигуры, заданной в параметрической форме

[vas60005596]

Здравствуйте! Имеется задача по вычислению площади фигуры, заданной в параметрической форме, пределы интегрирования даны.
x=2cos(1+cost); y=2sint(1+cost); 0 \leqslant t \leqslant 2 \pi
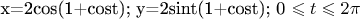
Использовал формулу S = \int\limits_{0}^{2 \pi } y(t)x'(t)dt
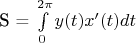
Далее нашел производную x'(t)=(2cost(1+cost))'=(2cost+2cos^{2}t)'=-2sint-4cost sint=-2sint(1+2cost)
Далее подставил это все под знак интеграла и преобразовал. Получилось
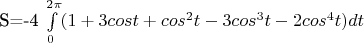
S=-4 \int\limits_{0}^{2 \pi } (1+3cost+cos^{2}t-3cos^{3}t-2cos^{4}t) dt. Проверял, вроде правильно. А дальше вообще никак не выходит... После интегрирования получаю одни синусы, и получается, что площадь равна 0. Подскажите, пожалуйста, где я допустил ошибку/ошибки??
F(x)=\int (1+3cost+cos^{2}t-3cos^{3}t-2cos^{4}t) dt=\int dt+3\int cost dt+\int cos^{2}tdt-3\int cos^{3}tdt-2\int cos^{4}tdt
\int dt=t+C
\3\int cost dt=sint+C
\int cos^{2}tdt=\int \frac{ 1+cos2t }{ 2 } dt=\frac{ 1 }{ 2 }\int (1+cos2t)dt=\frac{ 1 }{ 2 }(t+\frac{ 1 }{ 2 }sin2t)+C=\frac{ 1 }{ 2 }t+\frac{ 1 }{ 4 } sin2t+C
3\int cos^{3}tdt=3\int cos^{2}t costdt=3\int cos^{2}t d(sint)=3\int (1-sin^{2}t)d(sint)=3(sint-\frac{ cos^{3}t}{ 3 })+C=3sint-sin^{3}t+C
2\int cos^{4}tdt=2\int \frac{ 1+cos^{2}2t }{ 2 } dt=\int (1+cos^{2}2t)dt=t+\int cos^{2}2tdt=t+\int \frac{ 1+cos4t }{ 2 } dt=t+\frac{ 1 }{ 2 } \int (1+cos4t)dt=t+\frac{ 1 }{ 2 }t+\frac{ 1 }{ 8 }sin4t+C=\frac{ 3 }{ 2 }t+\frac{ 1 }{ 8 } sin4t+C
F(x)=t+3sint+\frac{ 1 }{ 2 }t+\frac{ 1 }{ 4 }sin2t-3sint+sin^{3}t-\frac{ 3 }{ 2 }t-\frac{ 1 }{ 8 }sin4t+C=\frac{ 1 }{ 4 } sin2t+sin^{3}t-\frac{ 1 }{8 }sin4t+C
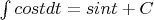
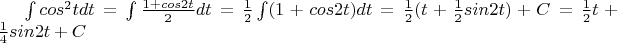
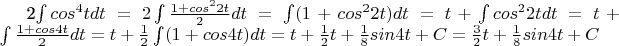
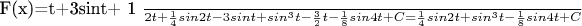
Вот.... Получились одни синусы, которые при подстановке 2\pi занулятся все. Подскажите, пожалуйста, где ошибка...

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);


Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.