Схождение ряда по признаку сравнения

[welovelain]

$$\sum\limits_{n=1}^\infty$$=$\frac{3^n+4^n}{5^n}$

Мне нужно определить (по признаку сравнения), сходится этот ряд или расходится. Видно, что он сходится, но как это доказать?

По признаку сравнения берем
0<=a(n)<=b(n)
Если "b" сходится, то "a" тоже сходится.
Если "a" расходится, то "b" тоже расходится.

Я не могу сообразить, что куда подставить. Сразу хочется взять $\frac{1}{5^n}$, как ряд геометрической прогрессии (который сходится) и подставить его, но он меньше, чем оригинальная формула, следовательно он будет "a", формула будет "b", а сходимость "a" не определяет сходимость "b". Как тут поступить?

-- 09.03.2015, 13:13 --

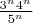
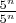
Ещё есть вариант типа 0<=$\frac{3^n4^n}{5^n}$<=$\frac{5^n}{5^n}$=1.
"b" равен 1, сходится, следовательно "a" сходится. Так можно?

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);


Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.