Собственно, моё (субъективное) доказательство:
Разделяй и властвуй
Пусть мы проверили

чисел на соответствие гипотезе, то есть все числа до

включительно удовлетворяют гипотезе Колатца.
Учитывая произвольность, потребуем, чтобы

было кратным

то есть
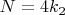
.
0) Все числа от

до
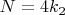
включительно удовлетворяют гипотезе Колатца
1) Рассмотрим числа
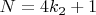
Числа являются нечётными, поэтому первое действие, согласно гипотезе, заключается в умножении на

и прибавлении

Имеем:
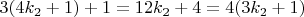
Полученное число кратно, как минимум,

После деления на

получим
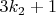
, которое удовлетворяет гипотезе Колатца, поскольку
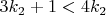
2) Рассмотрим числа
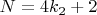
Числа являются чётными, поэтому первое действие, согласно гипотезе, заключается в делении на

После деления на

получим
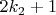
, которое удовлетворяет гипотезе Колатца, поскольку
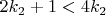
3) Рассмотрим числа
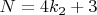
Числа являются нечётными, поэтому первое действие, согласно гипотезе, заключается в умножении на

и прибавлении

Имеем:
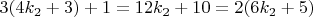
Число
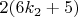
является чётным, после деления на

получается число
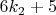
, которое является нечётным
Полученное число
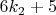
либо выводит нас в множество чисел, которые уже удовлетворяют гипотезе Колатца, либо в тот же самый набор чисел.
приравняем
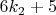
числу
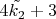
, таким образом мы определяем, что попали в то же самое множество чисел или вышли из него в множество чисел, для которых гипотеза Колатца уже доказана
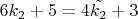
Получаем
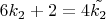
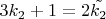
Откуда получаем, что при чётных

(включая

) величина
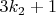
является нечётной, то есть выводит нас в числа, для которых гипотеза Колатца уже подтверждена, поскольку нечётная величина не может быть равна чётному
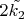
А при нечётных

мы попадаем в ту же последовательность
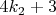
с той лишь разницей, что оставшиеся числа, для которых гипотеза Колатца не доказана описываются формулой
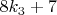
Эти числа являются нечётными, поэтому далее поступаем аналогичным образом, а именно: умножаем на

и прибавляем

, а далее тоже аналогично: Полученный результат делится на две группы
Первая выводит нас в числа, для которых гипотеза Колатца уже доказана;
Вторая выводит нас в числа, которые описываются формулой
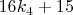
Так мы можем поступать сколько угодно раз, получая
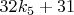
(остальные удовлетворяют гипотезе Колатца)
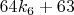
(остальные удовлетворяют гипотезе Колатца)
и т.д.
то есть для любого

, описываемого формулой
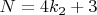
(для других

гипотеза выполняется в соответствии с пунктами 0, 1, 2) можно указать такое

(чётное

, включая

), что
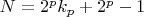
будет удовлетворять гипотезе Колатца, для других

(нечётных

) всегда можно провести переобозначения
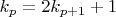
и перейти к
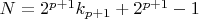
То есть для любого числа

можно найти соответствующее число

, в соответствии с которым оно при первой же итерации гипотезы Колатца будет выводится в множество чисел, для которых гипотеза Колатца верна.
-- Вс окт 05, 2025 01:22:38 --4)
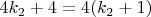
Что приводит нас к числу

, для которого гипотеза Колатца соблюдается
И т.д. по накатанной.