Гипотеза Колатца

[Lia]

Soul Friend в сообщении #1341458 писал(а):

У меня нет endorcement-а на arxiv.org, если я выложу здесь ссылку на pdf небольшой моей статьи про гипотезу Коллатца для вашего ознакомления или "рецензий", это будет считаться рекламой?

Будет. Soul Friend, задавайте такие вопросы не пространству, а любому действующему модератору раздела, пожалуйста. Остальные ответить Вам на него все равно не могут.

[Sender]

Soul Friend в сообщении #1341458 писал(а):

если я выложу здесь ссылку на pdf небольшой моей статьи про гипотезу Коллатца для вашего ознакомления или "рецензий"

По-моему, здесь принято в таких случаях создавать тему в дискуссионном разделе и размещать доказательство там, пользуясь TeX-движком форума.

[Soul Friend]

kotenok gav в сообщении #1341471 писал(а):

Никак

Во-во, я об этом. У меня в статье есть метод который может это делать, кому надо могу в ЛС скинуть ссылку.

[Someone]

Soul Friend в сообщении #1341479 писал(а):

Во-во, я об этом. У меня в статье есть метод который может это делать

А у меня это вызывает сильные подозрения.

[kotenok gav]

Soul Friend в сообщении #1341479 писал(а):

кому надо могу в ЛС скинуть ссылку.

Ну, кидайте свой метод "факторизации".

[Soul Friend]

Someone
kotenok gav
скинул ссылку

[kotenok gav]

Soul Friend
Что-то я не понял. Несколько формул без доказательства. Где написано "из этого следует что последовательность прийдет к 1"?

[Lia]

Soul Friend
Я не вижу уместным продолжение частной переписки на страницах форума.
Если Вам нужно что-то обсудить - или продолжайте обсуждать в ЛС, или выносите это наружу в установленном порядке.

[Soul Friend]

я не доказываю гипотезу, а раскрываю закономерности чисел-градин.

-- 26.09.2018, 00:12 --

Lia
хорошо. больше не буду.

[Neoguri]

Частичный результат по проблеме Коллатца:

https://terrytao.wordpress.com/2019/09/ ... ed-values/
https://arxiv.org/abs/1909.03562

[maxal]

Neoguri в сообщении #1414523 писал(а):

Частичный результат по проблеме Коллатца:

Научно-популярное изложение результата Тао:
https://www.quantamagazine.org/mathemat ... -20191211/

[Bizon]

Я решил рассмотреть гипотезу Коллатца в 6-тизначной системе счисления.
В этой системе четные числа заканчиваются на 0, 2, 4.
Нечетные числа заканчиваются на 1, 3, 5.
Допустим существует первое число, опровергающее гипотезу Коллатца. Назовем его $K$.
Очевидно, что $K$ - нечетное число. Посмотрим, что произойдет с последним разрядом этого числа при применении правила $3n+1$:
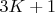
Если $K$ заканчивается на 1 (число вида $6a + 1$), то $3K+1$ будет заканчиваться на 4.
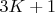
Если $K$ заканчивается на 3 (число вида $6a + 3$), то $3K+1$ будет заканчиваться на 4.
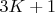
Если $K$ заканчивается на 5 (число вида $6a + 5$), то $3K+1$ будет заканчиваться на 4.
Числа заканчивающиеся на 4 после деления дают числа заканчивающиеся на 2 и 5.
Числа заканчивающиеся на 2 после деления дают числа заканчивающиеся на 1, 4 и 5.
Переходы значений последних разрядов показаны на схеме (по ссылке png картинка, красные стрелки - увеличение числа, синие - деление):
https://drive.google.com/file/d/1gRw9n_0atN4g0Ac81Ao1vAHk8gZPEdPy
Исходя из этой схемы сразу можно сделать несколько очевидных предположений:
1. Чисел заканчивающихся на 0 нет вообще, а число заканчивающееся на 3 может быть максимум одно (первое в последовательности).
2. Чисел заканчивающихся на 4 больше всего и их количество равно сумме чисел заканчивающихся на 5 и 2 (потому что все "четверки" разваливаваюся на "пятерки" и "двойки").
3. Чисел заканчивающихся на 1 меньше всего (поскольку к "единицам" приводят только некоторые из двух последовательных делений).
Осталось только доказать, что единственный замкнутый цикл, который приводит к увеличению ("пятерка" - "четверка" - "пятерка" - "четверка" -"пятерка" - и т.д.) не может быть бесконечным.

[Dmitriy40]

Bizon в сообщении #1683448 писал(а):

Осталось только доказать, что единственный замкнутый цикл, который приводит к увеличению ("пятерка" - "четверка" - "пятерка" - "четверка" -"пятерка" - и т.д.)

Это не так, цикл 4-2-1-4-5-4 тоже приводит к увеличению. Как и цикл 4-2-1-4-2-1-4-2-1-4-2-1-4-5-4-5-4-5-4. И множество других циклов, более длинных (например 7 циклов 4-2-1-4 и 5 циклов 4-5-4 или 11 циклов 4-2-1-4 и 8 циклов 4-5-4 и так далее).
Более того, таких комбинаций бесконечно много, для каждого количества циклов 4-2-1-4 найдётся минимально необходимое количество циклов 4-5-4, которое даст увеличение исходного числа.
Так что придётся доказывать не только бесконечность появления цикла 4-5-4, но и что их не меньше чем некая функция от количества циклов 4-2-1-4, а именно не менее чем $y(x)=\lceil x \log_{3/2} 4/3 \rceil$.

[MerkulovaLE]

Какая интересная тема, вставлю свои пять копеек:
1)

$F$-функция Коллатца

$F(2x-1)=(2x-1)3+1=6x-3+1=6x-2$

$F(6x-2)=3x-1$

Преобразуем формулу

$F(2x-1)=3x-1$

$F(2x)=x$

Теперь прибавим единицу к правой и левой части

$F_1(2x)=3x$

$F_1(2x+1)=x+1$

К результату тоже добавляем единицу:

$1+1=2$

$F_1(2)=3$

$F_1(3)=2$

$F_1$ зацикливается на $2$ и $3$

Возьмем обратную к $F_1$ функцию $F_2$

$F_2(3x)=2x$

$F_2(x+1)=2x+1$

$y=x+1$

$x=y-1$

$F_2(y)=2(y-1)+1=2y-1$

В итоге

$F_2(3x)=2x$

$F_2(x)=2x-1$

Чтобы доказать гипотезу Коллатца надо доказать, что $F_2$ от двойки дойдет до любого числа, большего двойки

2)
Функция Коллатца

$F(4x+3)=(4x+3)3+1=12x+10$

$F(12x+10)=6x+5$, нечетное число

$F(8x+1)=(8x+1)3+1=24x+4$

$F(24x+4)=6x+1$, нечетное число

$F(4x+1)=(4x+1)3+1=12x+4$

$F(12x+4)=3x+1$

Если $х$ – нечетное число, то $F(4x+1)=x$, который на следующем же шаге будет равен
$3x+1$. $F(8x+5)=2x+1$

Объединяем

$F(4x+3)=6x+5$

$F(8x+1)=6x+1$

$F(8x+5)=2x+1$

Вычитаем из обеих частей единицу и делим на 2

$F_1(2x+1)=3x+2$

$F_1(4x)=3x$

$F_1(4x+2)=x$

Довести надо до $\frac{(1-1)}{2}$, то есть до нуля. Тогда гипотеза Коллатца будет доказана.

3)

$F(x)=3x+1$, если х – нечетное

$F(2x)=x$

Умножим обе части на 3

$F_1(3x)=9x+3$

$F_1(6x)=3x$

Довести надо до $3$

Разделим $x$ на $3$

$F_2(x)=3x+3=3(x+1)$

$F_2(2x)=x$

Но $x$ должен делиться на $3,$ что достигается при первом умножении $х$ на три с добавлением тройки

Если в результате применения функции $F_2$ к положительным числам получается $3$, то гипотеза Коллатца доказана

4)

$F(2x-1)=3x-1$

$F(2x)=x$

$F(x2^{y}-1)=x3^{y}-1$

$x$ – нечетное число $= 2z+1$

$(2z+1)3^{y}-1=2z3^{y}+3^y-1=2z3^{y}+2(1+3+9+\ldots+3^{(y-1)})$

Делим на $2$

$z3^{y}+1+3+\ldots +3^{(y-1)} = (((3z+1)3+1)3+\ldots +1)$

Идет чередование четных и нечетных значений в скобках. Если значение нечетное, то $3x+1$ – следующий шаг, то есть, если $4x+3$ сходится к единице, то или $2x+1$, или $8x+7$ – тоже сходится к единице. А если $4x+3$ не сходится к единице, то или $2x+1$, или $8x+7$ не
сходится.

$4$ копейки получилось…