Ну, во-первых, понять таки можно, хоть и непросто. Программёж — занятие творческое (лично я в этом убеждён), и в нём таки встречаются непростые задачи.
по другим то условиям можно понять
Не скажите. Просто задачку мы рассматриваем даже не учебную. К примеру, безобиднейший

ведёт не просто, как в нашем случае, к приписыванию
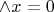
— если

у нас участвовал в вычислениях, надо просмотреть входящее условие и исключить его оттуда. В общем, всё решаемо, но не механически.
Во-вторых, задача построения программы по пред- и постусловиям, насколько знаю, не стоит. Либо (правильный способ) пишем программу и одновременно все эти условия, либо по программе пишем условия.