Вокруг "Цитатника"

[realeugene]

warlock66613 в сообщении #1430575 писал(а):

квантовых событий

А это что такое? Если без привлечения "классической реальности", так как обсуждаемый "механизм" находится вне классической реальности.

[warlock66613]

realeugene в сообщении #1430584 писал(а):

А это что такое?

Событие - результат измерения квантовой системы. "Спин электрона оказался направленным вверх", например.

[realeugene]

warlock66613 в сообщении #1430585 писал(а):

Событие - результат измерения квантовой системы. "Спин электрона оказался направленным вверх", например.

Но по этому определению все события находятся внутри классической реальности. Но такие события принципиально непредсказуемы, т. е. подобный "механизм", их "определяющий", невозможен.

[warlock66613]

realeugene в сообщении #1430587 писал(а):

Но такие события принципиально непредсказуемы, т. е. подобный "механизм", их "определяющий", невозможен.

Не так уж трудно придумать какой-нибудь скрытый механизм (скрытые параметры), принципиально ненаблюдаемый, но определяющий эти события.

[arseniiv]

Кстати интересно, насколько простую (и маленькую) игрушечную модель квантового мира можно придумать, где можно будет иметь существенно классическую подсистему (чтобы можно было там внутри что-то измерять; и по желанию прикрутить туда снаружи такого «демона Борна»).

[warlock66613]

arseniiv, вопрос интересный. Как я понимаю, он сводится к задаче найти минимальную модель с декогеренцией и квантовым дарвинизмом.

-- 17.12.2019, 01:18 --

Вот только никакого демона уже и не нужно будет. Достаточно постулировать, что классическая сиситема соответствует ветви Мультивселенной с большой амплитудой, то есть неисключительной ветви, и правила Борна уже можно вывести.

[arseniiv]

warlock66613 в сообщении #1430596 писал(а):

Достаточно постулировать, что классическая сиситема соответствует ветви Мультивселенной с большой амплитудой, то есть неисключительной ветви

А обязательно будет только одна такая?

[realeugene]

warlock66613 в сообщении #1430596 писал(а):

Достаточно постулировать, что классическая сиситема соответствует ветви Мультивселенной с большой амплитудой,

За счёт чего выживает одна веть с большой амплитудой в условиях унитарной эволюции и прибора, спроектированного максимально точно и однозначно откликаться на каждое собственное состояние измеряемой величины? Боюсь, чтобы статистика была правильной, мы иногда должны оказываться в маловероятных копиях Вселенной.

[warlock66613]

arseniiv в сообщении #1430598 писал(а):

А обязательно будет только одна такая?

Нет, наоборот, такая точно не одна.

[arseniiv]

Но с этим как-то можно справиться?

[warlock66613]

realeugene в сообщении #1430610 писал(а):

Боюсь, чтобы статистика была правильной, мы иногда должны оказываться в маловероятных копиях Вселенной.

Результаты экспериментов в ветви с большой амплитудой дают как раз правильную статистику.

arseniiv в сообщении #1430613 писал(а):

Но с этим как-то можно справиться? :-)

Кажется, нет.

[realeugene]

warlock66613 в сообщении #1430746 писал(а):

Результаты экспериментов в ветви с большой амплитудой дают как раз правильную статистику.

А где эта теория изложена с расчётами?

[warlock66613]

realeugene, 'это должно быть в статье N. Graham The Measurement of Relative Frequency. Найти её онлайн у меня не получается.

-- 18.12.2019, 02:53 --

А это цитата из моей любимой книги H. Zeh The physical basis of the direction of time, которая и ссылается на вышеупомянутую работу:

Цитата:

Graham (1970) therefore considered series of N equivalent measurements ($N$ subsequent branchings - similar to series of decay events discussed at the end of Sect. 4.5). He was then able to demonstrate that the total norm of all those of the resulting Everett branches which represent series of outcomes that differ significantly from the Born rule must become extremely small, and vanish in the limit $N \to \infty$ (see also Jammer 1974). While this result permits an elegant formulation of the probability postulate (by assuming merely that we happen to live in an Everett branch of not extremely small norm), this assumption is still completely equivalent to what is to be derived*.

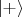
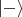
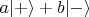
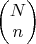
* This may be illustrated by the example of results obtained for $N$ subsequent measurements distinguishing between spin states $|+\rangle$ and $|-\rangle$ in $N$ identical initial superpositions $a|+\rangle + b|-\rangle$. Since the number of branches which contain $n$ ‘spinups’, say, is then statistically given by the binomial coefficient $\begin{pmatrix} N \\ n \end{pmatrix}$ regardless of the values of the coefficients $a$ and $b$, the distribution of measurement outcomes $n$ over many such series of $N$ measurements, $p_N(n)$, would form a Poisson distribution centered at the required value if and only if the probability for each branch is assumed to be given by its norm $|a|^{2n} |b|^ {2(N-n)}$. This is precisely Born’s probability rule. (Example provided by Erich Joos.)

[realeugene]

warlock66613

то есть это всё а рамках интерпретации Эверетта? Ветвящихся классических миров может быть множество, но существенно неклассический мир маловероятен? В общем-то правило Борна выводится ещё у Эверетта.

[warlock66613]

realeugene в сообщении #1430784 писал(а):

В общем-то правило Борна выводится ещё у Эверетта.

Эвереттовский вывод содержит кольцо - неявно опирается на доказываемое утверждение. (Это общепризнано.) А удовлетворительного вывода правил Борна нет и по сей день.

-- 18.12.2019, 11:54 --

realeugene в сообщении #1430784 писал(а):

то есть это всё а рамках интерпретации Эверетта?

Ну в общем да.

realeugene в сообщении #1430784 писал(а):

Ветвящихся классических миров может быть множество, но существенно неклассический мир маловероятен?

Я бы сказал, что он имеет малую амплитуду. Если считать, что квадрат этой амплитуды даёт некую вероятность (непонятно чего), то да, он маловероятен.