общая топология

[brachypelma]

Открытое инъективное отображение является вложением (в смысле индуцированной топологии)
Как доказать такого рода утверждение?
Мои рассуждения:
Пусть заданы топологические пространства $X$ и $Y$, $f: X $\mapsto$ Y$ открыто и инъективно, необходимо доказать что $f: X $\mapsto$ f(X)$ гомеоморфизм. То что это отображение биективно очевидно, в силу инъективности, поэтому существует и обратное отображение, в свою очередь в силу открытости отображения $f: X $\mapsto$ f(X)$ обратное к нему будет непрерывным.
Теперь собственно вопросы, нет идей как доказать что само $f: X $\mapsto$ f(X)$ непрерывно (без этого док-ва у меня не получается гомоморфизм). Единственное что приходит в голову, как то покрутить то что топология на $f(X)$ индуцированна в $Y$. 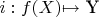Логично что тут как то его нужно использовать, но кроме того что индуцированная топология является самой грубой из всех топологий, таких что $i: f(X) $\mapsto$ Y$ непрерывно я не знаю больше свойств индуцированных топологий.

-- 10.02.2015, 22:44 --

Пересмотрел записки лекции, все отображения подразумевались непрерывными, поэтому не нужно доказывать непрерывность $f: X $\mapsto$ f(X)$ т.к. оно по условию непрерывно, поэтому это и гомеоморфизм.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы): Каждая формула должна а) начинаться с доллара, б) заканчиваться долларом, в) других долларов не содержать.

- Упорядочьте Ваши попытки решения и постановку задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.