Дано.
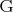
абелева группа,

ее "разностное множество" (difference set),

.
Доказать, что для любого простого числа

существует

, такой что

, где

и

.
Комментарий. Задали тут сыну, я пытался, но безуспешно. Видимо, доказательство может быть придумано на основе знаний книги D. Huges, C. Piper, Projective Planes, 1973. По крайней мере так советовал его доцент.

ее "разностное множество"
А что это? Приведите определение.
В формулировке задачи операция обозначена умноженем, хотя, как мне заметели, обычно для абелевых групп используется аддитивная операция. Чтобы не нарушать номенклатуру доцента продолжу использовать "умножение".
Определение.
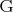
конечная абелева группа группа порядка

. Ее подмножество

из

элементов называется "разностным множеством" (русский перевод я посмотрел в интернет-словаре, в оригинале задачи - Differenzmenge или difference set) для
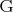
, если любой неединичный элемент

может быть представлен единственным образом в виде

где

.