Пи спираль (?)

[Stas_S]

Лет 25 тому назад попалась мне задачка из сборника олимпиадных , России 1916 года.

Суть такова: построение на плоскости. (№№№ - номера построений).

№1 - Из точки "О" строим единичный вектор. (вертикально, юг-север)
№2 - К концу первого вектора "пристраиваем" единичный вектор, перпендикулярный первому.
(допустим, по часовой стрелке)
- Соединяем начало первого (точку О) с концом второго, получаем вектор-гипотенузу, "квадрат" которой равен номеру построения, натуральному числу 2.
№3 - К концу гипотенузы пристраиваем Единичный вектор, перпендикулярно гипотенузе, соединяем точку О с концом третьего единичного вектора, получаем гипотенузу, квадрат которой равен 3.
№4 - ......... и так далее....
Всякий раз мы будем получать гипотенузу, квадрат которой равен номеру построения.

Что спрашивалось в той задаче я не припомню, потому как меня заинтересовал сам "принцип построения", и я решил продолжать построения до "посинения".

В итоге получил некую "спираль". Не обременяя себя доказательствами, взял в руки калькулятор (компьютера тогда не было ) и вот, оказалось, что расстояние между соседними витками этой "спирали" стремится к нашему родному числу $\pi$. Возьмется ли кто основательно, доказательно опровергнуть или подтвердить "показания калькулятора". Excel с его 15 значениями подтверждает, но...
(Возможно эта "спираль" уже стала "достоянием" математики, но мне о том неведомо. Может быть, у нее есть еще какие-либо интересные свойства). Спасибо!

[gris]

Ну если навскидку в полярных координатах, то получаем угол, равный частичной сумме из арксинусов обратных квадратных корней и радиус из очередного квадратного корня. Ряд, естественно, расходится, спираль разматывается. Наверное, можно оценить с помощью интеграла частичные суммы и получить удлинение радиуса за один виток.
Впрочем, на достаточном удалении можно просто оценить приращение угла и приращение радиуса, пользуясь простейшими эквивалентностями. Вроде бы всё получается, как Вы и предположили. Скорость удлинения радиуса в два раза меньше скорости удлинения вектора. То есть пока угол увеличится на оборот, то есть $2\pi$ радиус удлинится на половинку, то есть $\pi$.

[Stas_S]

Я шел таким путем. Построение № 1 000 000. Гипотенуза - 1 000. Учитывая вырождение многоугольника в окружность, умножил 6.28 на 1000. Прибавил 6280 к 1 000 000 "=" 1 006 280 и извлек корень . Получил 1 003,14 -1 000 "=" 3,14. В Excel просто ввел формулы и автоматом вычисляет. Вот результат работы,
построение № 1 000 000 000 000 000 000 - 3,14159262180328. Точность - 99,999998988204%
Конечно хотелось бы красивого доказательства, но я уже "устарел", "обленился", а потому "рассчитываю" на молодые умы.

[Stas_S]

В идеале это напоминает "сматывание (или разматывание) нити" со стержня единичного диаметра...

[gris]

Чем дальше, тем ближе будут точки к архимедовой спирали с шагом $\pi$, которая будет приближаться к <чуть повёрнутой> инволюте к окружности, с которой Вы сматываете нить. Всё это действительно имеет место. Для миллионной точки вполне можно провести и точные (разумеется в границах точности расчётов самой Эксельки) расчёты. На самом деле, полный оборот после миллионной точки наступит не за 6280 шагов, а за 6294 с небольшим. Интерполируя, можно получить расстояние между нужными точками: 3,1415929145. Как видите, значение весьма близко к $\pi$. У Вас получилось тоже хорошо, но Вы необоснованно заменили участок спирали окружностью. Предположение верное, но расчёт производился именно для приближённой модели. Конечно, мы на ней будем приближаться к $\pi$, но это, увы, не доказательно.
Анализируя ряд $\sum\arcsin\dfrac1{\sqrt n}$, мы можем получить доказательство и оценки, но, вероятно, существует и школьный вариант достаточно строгого рассуждения.

[Stas_S]

gris в сообщении #972446 писал(а):

Конечно, мы на ней будем приближаться к $\pi$, но это, увы, не доказательно.

Если взять два ряда (пусть расходящихся), но показать, что разность элементов с одинаковыми №№ номерами сходится к Пи..... Только вот за что зацепиться для начала? ... Две соседние гипотенузы?

[gris]

Вт картинка.

Мы видим, что $\sin\angle A_n=\dfrac1{\sqrt {n+1}}$, то есть $\angle A_n=\arcsin\dfrac1{\sqrt {n+1}}$
Можно рассмотреть это дело в полярных координатах.
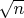
Для n-ной точки длина радиус-вектора равна $\sqrt n$, а угол равен сумме углов $\sum\limits_{i=2}^n A_{i-1}=\sum\limits_{i=2}^n \arcsin\dfrac1{\sqrt {i}}$
Вот так:
$1:\,(1,0)$
$2:\,\left(\sqrt2,\arcsin\dfrac1{\sqrt2}\right)$
$3:\,\left(\sqrt3,\arcsin\dfrac1{\sqrt2}+\arcsin\dfrac1{\sqrt3}\right)$
Вот это дело легко запихать в Эксель и посмотреть, что там происходит.

№     R        fi        Dr      Dfi
1   1,0000   0,0000   0,0000   0,0000
2   1,4142   0,7854   0,4142   0,7854
3   1,7321   1,4009   0,3178   0,6155
4   2,0000   1,9245   0,2679   0,5236
5   2,2361   2,3881   0,2361   0,4636
6   2,4495   2,8087   0,2134   0,4205
7   2,6458   3,1963   0,1963   0,3876
8   2,8284   3,5576   0,1827   0,3614
9   3,0000   3,8975   0,1716   0,3398
10   3,1623   4,2192   0,1623   0,3218
11   3,3166   4,5255   0,1543   0,3063
12   3,4641   4,8183   0,1475   0,2928
13   3,6056   5,0994   0,1414   0,2810
14   3,7417   5,3699   0,1361   0,2705
15   3,8730   5,6311   0,1313   0,2612
16   4,0000   5,8838   0,1270   0,2527
17   4,1231   6,1287   0,1231   0,2450
18   4,2426   6,3667   0,1195   0,2379
19   4,3589   6,5981   0,1163   0,2315
20   4,4721   6,8237   0,1132   0,2255
21   4,5826   7,0437   0,1104   0,2200

Первый оборот на 17-й точке, второй на 55-й, третий на 110-й, четвёртый на 190.
Но и просто по ряду видно, что он эквивалентен ряду из обратных квадратных корней и расходится. Интегрируя, можно получить приближения достаточно далёких кусков ряда.
Тогда, решив уравнение (арксинусы можно уже отбросить) $\sqrt {N+x}-\sqrt N=2\pi$, мы увидим, что при больших $N$ полный поворот происходит примерно через $2\pi\sqrt N$ шагов. А удлинение радиуса будет приближаться к $\pi$.
Так что Ваши предположения верны!

[Stas_S]

№ 1 000 000 000 000 000 000
Взял свой же пример. Длина окружности этого построения (радиус 1 000 000 000,0 )
равна 6 283 185 307,17959, а длина окружности "через оборот" (радиус 1 000 000 003,14159 ) равна 6283185326,91879. Разность - 9,86960411071777, т.е. стремится к $\pi^2$ .... Т.е., на этом этапе уже можно (?) пренебрегать спиралью в пользу окружности, т.к. ошибка в количестве построений для замыкания круга не превысит 10. Никогда! (спасибо за картинку, я еще не успел освоить).

[gris]

У Вас какая-то ошибка в расчётах, либо пренебрегать спиралью рановато. Известно (хотя и не обще-), что после увеличения радиуса окружности на $\pi$ её длина увеличивается на $2\pi^2$. Удивительно, как возникают такие нелинейные эффекты.

[Stas_S]

gris в сообщении #972694 писал(а):

У Вас какая-то ошибка в расчётах, либо пренебрегать спиралью рановато. Известно (хотя и не обще-), что после увеличения радиуса окружности на $\pi$ её длина увеличивается на $2\pi^2$. Удивительно, как возникают такие нелинейные эффекты.

Точно, так и есть. Шутки Эксцеля. Там в клетке формула стояла "/2", а я оттуда и скопировал "автоматом".
19,7392082214355 - а этот из правильной клетки, Два Пи квадрат. Спасибо, будем пренебрегать, начиная с 36 нулей. (Я Вам в "личку" письмо отправил ....)

[Stas_S]

На днях случилась у меня беседа о математике(и не только о ней). Число Пи не упоминалось ни разу. Но, видимо, "конструкция беседы" содержала Пи. Из этой беседы вышло еще одно построение на плоскости. Поэтому 99% принципа построения я "присваиваю" собеседнику!

1). На плоскости из точки "О" откладываем 4 единичных вектора (по осям). Нумеруем их против часовой стрелки, 1,2,3,4. Перемножаем последовательно "№1на№2", "2на3", "3на4", "4на1". Произведение векторное!! Суммарный Псевдовектор (длина) равен 4.

2). Делим углы между векторами пополам. На биссектрисах, из точки "О", откладываем единичные векторы. Теперь их 8. Нумеруем их против час. стрелки (с нашего первого №1). Перемножаем векторно.

Псевдовектор равен $8\sin45$

3). Опять же, - пополам, откладываем, нумеруем, умножаем .... до "посинения"...

........

№ ..Оччень большой номер построения). Мы приходим к радиусу 2 , и длине псевдовектора $4\pi$.

А если наши векторы - "половинки" Единичного - имеем псевдовектор $\pi$
Если же корень из 2 - получаем $2\pi$.

Чувствую, но доказать-показать, - попрошу читателей.

[gris]

Вероятно, стоило бы рассматривать дело в комплексном пространстве, но я по простоте изложу на пальцах. Так как все векторы единичные, ориентация пар хорошая, углы в каждом произведении одинаковые, то модуль суммы векторных произведений на $n$-ном шаге равен $M_n=2^{n+1}\cdot \sin\left(\dfrac {2\pi}{2^{n+1}}\right)$
Рассматривая процесс в неограниченном развитии, используя Первый Замечательный Предел, мы получим $M=\lim\limits_{n\to \infty} M_n=2\pi$.
Я, наверное, не так понял фразу о радиусе некоторой окружности, но если все векторы единичные, то их концы лежат на единичной окружности.
С учётом этого Вы абсолютно правы.
Отмечу, кстати, что хотя Ваши частные построения и можно выполнить циркулем и линейкой, предельное построение "не считается" и отрезок длины $\pi$ при данном единичном построить нельзя, так как нельзя, что не умаляет Вашего интересного результата.

[Stas_S]

Исхожу из следующего утверждения:
""длина вектора С равна произведению длин векторов А и В на синус угла между ними"" (т.е. - площади ромба в нашем случае).

При малых углах (или больших номерах построений), наша "элементарная" площадь - есть площадь "узенького", вытянутого ромба, и его бОльшая диагональ стремится к 2. Это и есть предполагаемый радиус. Конечно, в этом построении нет речи об отрезке равном $\pi$ в плоскости построения. Речь о суммарной площади, равной длине псевдовектора. Вопрос в том, будет ли суммарная площадь равна площади окружности радиуса 2?

[Stas_S]

gris в сообщении #976028 писал(а):

Вероятно, стоило бы рассматривать дело в комплексном пространстве, ...

Можно, видимо, и не торопиться с комплексной областью, если свести "дело" к вычислению объема цилиндра, который по моим "расчетам" равен $16\pi^2$....

[Stas_S]

Мой Эксцель соглашается с Вами, gris, и выдает площадь, равную $2\pi$, а значит радиус стремится к $\sqrt{2}$. Вынужден и я согласиться. (иллюзия ).
А значит объем "цилиндра" равен $4\pi^2$

В результате построения получается "шестеренка" радиуса 2, "сплошное тело" которой, радиуса 1. Эффективный радиус (если говорить о площади "шестеренки" вместе с зубьями) равен $\sqrt{2}$