Фортран. Метод монте карло

[Kaila_M]

Добрый день, новичок в программе фортран . Я хотела бы попросить помочь разобраться с методом Монте-Карло. Необходимо набрать программу на Фортране.

Let $f(x)={e}^{{-x}^{2}}$ and [a,b] = [0,1]. The true value of Q is $\frac{\sqrt{\pi }}{2}$ erf(1) = 0.7468241.
Write a Fortran program for implementing $\tilde{Q}=\sum_{i=1}^{N}\frac{f({x}_{i})}{g({x}_{i})}$ in the following cases:

a) g(x) = 1, which is ‘brute force’ integration, i.e. no importance sampling;
b) g(x) = a exp(- x), where a is a proper normalisation constant.

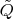
Tabulate the values of $\tilde{Q}$ in each of these two cases, together with their relative differences from the true value Q, as a function of N. What is the reasonable value of N for each case? Which of these two alternatives is to be preferred at relatively low values of N?

Thank you!


Начала я так
For a)

q=0.7468241    !данное значение
n=100                        !number of distribution
iseed=3124356
s=0
do i=1.n
x=rand(iseed)
s=s=exp(-x**2)
end do
s=s/n
r=s/q-1
write(*,*) s,r
end

Правильно ли?

[Toucan]

Тема перемещена из форума «Программирование» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.