Живёт ли наш мир по вероятностным законам?

[мат-ламер]

С точки зрения копенгагенской интерпретации квантовой механики, которой придерживаются многие физики, наш мир строго детерминирован. Строго детерминирована эволюция волновой функции Вселенной. Случайность же возникает в процессе измерения каких-то характеристик элементарных частиц квантового мира. При этом волновая функция Вселенной испытывает коллапс. Меня такая интерпретация не устроила. Были попытки представить наш мир как случайный процесс, но эти попытки противоречат экспериментам и от них отказались. В данном посту позволю себе попытку их реабилитации. Почему же они провалились? Дело в том, что в квантовом мире свои понятия о вероятности. В нашем мире вероятность задаёт действительным числом. Также плотность распределения случайной величины задаётся действительным числом. В квантовом мире (ИМХО) вероятность задаётся комплексными числами. Если случ. величина дискретна, то сумма квадратов модулей вероятностей исходов равна единице. Если случайна величина непрерына, то интеграл от квадрата модуля плотности распределения этой случ. величины равна единице. Т.о. Вселенную мы можем понимать как случайный процесс, и мы наблюдаем какую-то реализацию его. Электрон в атоме можно будет представить себе также как случайный процесс. При этом квантовая вероятность нахождения электрона в какой-то точке равна значению волновой функции электрона в данной точке. Волновая функция и есть квантовая плотность распределения случ. величины. Тем самым мы отождествляем электрон с его волновой функцией. Чтобы не путать квантовую вероятность с человеческой, следует квантовую вероятность назвать амплитудой вероятности или даже просто амплитудой. Например, при определении фейнмановского интеграла по траекториям можно полагать, что частица с какой-то амплитудой полетит по одной траектории, а с какой-то амплитудой полетит по другой траектории. (В то время, как тут на форуме объяснялось, что часть электрона полетит по одной траектории, а часть по другой, что меня не совсем удовлетворило). Разумеется всё предлагаемое не отменяет никакой формулы квантовой механики, а лишь касается её интерпретации, по поводу которой до сих у учёных нет единого мнения и продолжаются споры.

[Sicker]

а можете пожалуйста какой-нибудь вопрос или предмет, предмет обсуждения сформулировать, пожжалуйста

[Cos(x-pi/2)]

мат-ламер в сообщении #964126 писал(а):

В квантовом мире (ИМХО) вероятность задаётся комплексными числами. Если случ. величина дискретна, то сумма квадратов модулей вероятностей исходов равна единице.

Неверно! (Почитайте учебники-то, ёлы-палы...). В квантовой теории наблюдаемой случайной величине $f$ со спектром значений $f_1,\, f_2,\,...\, f_k, \,...\, f_N$ сопоставляются комплексные величины $A_1,\,A_2,\,...\,A_k,\,...\, A_N$, (уже давным давно называемые амплитудами вероятности) так, что вероятность $P_k$ обнаружить значение $f=f_k$ равна $|A_k|^2$. Это ведь легко запомнить - вероятность равна не амплитуде вероятности, а квадрату модуля амплитуды:

$P_k=|A_k|^2$ .

И единице равна вовсе не сумма квадратов модулей вероятности, а сумма вероятностей:

$P_1+...+P_N = 1$ .

Нет в квантовой теории комплексных вероятностей, есть обычные вероятности: $0\le P_k \le 1$. При сопоставлении теории с экспериментом считается, что экспериментальной оценкой для для $P_k$ является $n_k/n,$ где $n_k$ - количество испытаний, в которых при измерении величины $f$ обнаружилось k-ое значение ($f=f_k$) из всего спектра возможных значений, $n>>1$ - суммарное количество испытаний. На этом этапе всё обстоит как с классическими вероятностями.

Квантовая специфика появляется только на том этапе, когда в теории хотят вывести из набора амплитуд $A_k$ набор амплитуд $\Psi_x$ для другой случайной величины, скажем $g,$ со спектром $g_1,\, g_2,\,...\, g_x, \,...\, g_N$. Вероятность обнаружить $g=g_x$ равна квадрату модуля амплитуды вероятности: $|\Psi_x|^2.$ Квантовый принцип суперпозиции при этом гласит, что:

$\Psi_x=\sum_k \psi_{xk}A_k$ ,

где двухиндексные амплитуды $\psi_{xk}$ не зависят от одноиндексных и определяются сугубо свойствами величин $f$ и $g$. Далее, легко убедиться, что из условия нормировки вероятностей

$|\Psi_1|^2+...+|\Psi_N|^2=1$

следует свойство унитарности матрицы, составленной из комплексных величин $\psi_{xk}.$ Поэтому должна существовать обратная матрица (её элементы есть $\psi_{xk}^*$), позволяющая обратить линейные соотношения между одноиндексными амплитудами:

$A_k=\sum_x \psi_{xk}^* \Psi_x$ .

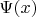
Бесхитростная линейная алгебра. В пределе с $N \to \infty$, для случая, например, когда спектр $f$ дискретный, а спектр $g$ непрерывный (так что и номер $x$ становится непрерывной переменной), эта схема сводится к формулам разложения "волновой функции" $\Psi(x)$ по "собственным функциям" $\psi_k(x)$ "оператора физической величины" $f$:

$\Psi(x)=\sum_k A_k \psi_k(x)$ ,

где:

$A_k=\int{dx} \, \psi_k(x)^* \, \Psi(x)$ .

При этом, как ясно из исходных определений, по-прежнему:

$|A_k|^2$ есть вероятность обнаружить $f=f_k$ у квантового объекта "в состоянии с волновой функцией" $\Psi(x)$,

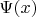
и

$|\Psi(x)|^2$ есть распределение вероятности для непрерывной случайной величины $g$. Если в качестве "номера" $x$ выбрать сами значения $g(x),$ то речь идёт о распределении вероятности для $x.$

Это набросок схемы исчисления вероятностей в КМ (в детали, такие как случаи с вырождением, в конкретику операторов, связь их с группами симметрии, про зависимость амплитуд от времени, и т.п. - здесь не вдаюсь). Главное: амплитуды вероятности и свойство физ. величин флуктуировать заложены в эту теор. схему изначально, так что никакой дополнительной "вероятностной интерпретации" этого формализма не требуется.

[Munin]

мат-ламер в сообщении #964126 писал(а):

С точки зрения копенгагенской интерпретации квантовой механики, которой придерживаются многие физики, наш мир строго детерминирован.

Ну, если даже в первом предложении неверное утверждение, то стоит ли дальше читать?

[мат-ламер]

Cos(x-pi/2)
Хотел ответить на ваш пост и уж не знаю чего сказать. Всё, что вы написали - это из-за путаницы в терминологии. Может быть вы потрудитесь ещё раз не спеша прочитать мой пост, так всё бы прояснилось. Я действительно употребил термин вероятность в квантовом смысле. Но затем, чтобы не было путаницы заменил этот термин амплитудой. Если же возражения у вас всё равно остаются, то обязуюсь подробно прокомментировать каждое ваше возражение, и показать где именно происходит путаница в терминологии.

-- Вс янв 18, 2015 19:07:42 --

Sicker в сообщении #964219 писал(а):

а можете пожалуйста какой-нибудь вопрос или предмет, предмет обсуждения сформулировать, пожжалуйста

Пожалуйста. Предложена новая интерпретация квантовой механики.

-- Вс янв 18, 2015 19:10:02 --

Munin в сообщении #964258 писал(а):

мат-ламер в сообщении #964126 писал(а):

С точки зрения копенгагенской интерпретации квантовой механики, которой придерживаются многие физики, наш мир строго детерминирован.

Ну, если даже в первом предложении неверное утверждение, то стоит ли дальше читать?

Вы уж дочитайте хотя бы первые четыре предложения, а уж потом говорите о верности и неверности первого предложения. Да и цитируйте уже тогда сразу четыре предложения.

-- Вс янв 18, 2015 19:16:13 --

Cos(x-pi/2)

мат-ламер в сообщении #964126 писал(а):

В квантовом мире (ИМХО) вероятность задаётся комплексными числами. Если случ. величина дискретна, то сумма квадратов модулей вероятностей исходов равна единице.

Cos(x-pi/2) в сообщении #964250 писал(а):

Неверно! (Почитайте учебники-то, ёлы-палы...). В квантовой теории наблюдаемой случайной величине $f$ со спектром значений $f_1,\, f_2,\,...\, f_k, \,...\, f_N$ сопоставляются комплексные величины $A_1,\,A_2,\,...\,A_k,\,...\, A_N$, (уже давным давно называемые амплитудами вероятности)

мат-ламер в сообщении #964126 писал(а):

Чтобы не путать квантовую вероятность с человеческой, следует квантовую вероятность назвать амплитудой вероятности или даже просто амплитудой.

Теперь читаем цитируемое первое предложение с учётом моей второй цитаты и получаем ровно то, что написали вы.

[Cos(x-pi/2)]

мат-ламер в сообщении #964313 писал(а):

Всё, что вы написали - это из-за путаницы в терминологии. Может быть вы потрудитесь ещё раз не спеша прочитать мой пост, так всё бы прояснилось. Я действительно употребил термин вероятность в квантовом смысле

Этот "квантовый смысл" Вы в своём тексте сами же ввели, запутав терминологию, и от своей же этой путаницы дальше попытались избавиться. Нигде в книгах по КМ такой путаницы не было и нет: посмотрите хотя бы ФЛФ (аж ещё в 1960-х годах издавались - там с самого начала речь идёт о комплексных амплитудах и о том, что вероятность это квадрат модуля амплитуды. Так что, "путаница", с которой Вы боретесь, это ваше же личное изобретение здесь, на этой страничке форума.

[Munin]

мат-ламер в сообщении #964313 писал(а):

Вы уж дочитайте хотя бы первые четыре предложения, а уж потом говорите о верности и неверности первого предложения.

Первое вопиюще неверно само по себе.

[Nemiroff]

Cos(x-pi/2) в сообщении #964320 писал(а):

Так что, "путаница" с которой Вы боретесь, это ваше же личное изобретение здесь, на этой страничке форума.

Ну чего вы сразу нападаете? Изобретение так изобретение — в изобретении ищут внутренние противоречия, а не несвязность с текущим пониманием. Вон, у Теренса Тао есть статья в блоге про экзотическое расширение теории вероятностей. https://terrytao.wordpress.com/2010/02/ ... obability/

[Munin]

мат-ламер в сообщении #964126 писал(а):

Меня такая интерпретация не устроила.

Если вам не нравятся законы природы, попробуйте переселиться в какую-нибудь другую реальность. Наиболее надёжное средство - галлюциногенные препараты. В последнее время набирает популярность другое средство: телевизор.

[arseniiv]

мат-ламер в сообщении #964313 писал(а):

Пожалуйста. Предложена новая интерпретация квантовой механики.

И в чём она состоит? Уж извините, стартовый пост — действительно каша ещё та. Я попытался его несколько раз почитать в разные стороны, но не помогло.

А, перечитал ещё раз, стало полегче.

Nemiroff в сообщении #964331 писал(а):

Вон, у Теренса Тао есть статья в блоге про экзотическое расширение теории вероятностей.

По-моему, это к словам мат-ламер не очень относится.

мат-ламер в сообщении #964126 писал(а):

Тем самым мы отождествляем электрон с его волновой функцией.

А как это относится к интерпретациям?

[мат-ламер]

Cos(x-pi/2) в сообщении #964320 писал(а):

Нигде в книгах по КМ такой путаницы не было и нет: посмотрите хотя бы ФЛФ (аж ещё в 1960-х годах издавались - там с самого начала речь идёт о комплексных амплитудах

А я поясняю, в чём истинный смысл комплексных амплитуд (и волновых функций). Если глубинный смысл этих понятий вас не волнует, и вы их принимаете такими какими они есть, то всё хорошо. Ничего не вижу страшного в том, что кто-то да и задумается, а что в сущности это такое?

[arseniiv]

Ну и какой у них глубинный смысл-то?

[мат-ламер]

arseniiv в сообщении #964339 писал(а):

Ну и какой у них глубинный смысл-то?

Ещё раз не торопясь читаем мой первый пост. Амплитуда - это вероятность. Но это не та вероятность, к которой мы привыкли. А это вероятность, в том понимании, в котором её понимает квантовый мир. И трудность в том, что понятия квантового мира не совпадают с нашими привычными понятиями. В следствие чего физики напридумали много терминов, толком не поняв, что они обозначают. Хотя проводить вычисления с ними научились. А волновая функция - это плотность распределения случайной величины. Опять же случайная величина понимается в квантовом смысле, а не в смысле. в котором мы привыкли.

[arseniiv]

Ну да, так становится всё сразу же понятно и ясно.

Вы надеялись получить смысл путём простого переобозначения, честно?

[Munin]

мат-ламер в сообщении #964342 писал(а):

Амплитуда - это вероятность. Но это не та вероятность, к которой мы привыкли. А это вероятность, в том понимании, в котором её понимает квантовый мир.

Ну и в чём смысл этого заявления?

Аксиомам вероятности не удовлетворяет. И всё.