Ошибка в оценке выигрыша/проигрыша при обмене конвертами. Ваши расчеты используют предположение о равновероятности обнаружения в соседнем конверте как

, так и

. Именно это предположение и неверно.
О, так понятнее!Только это не мои расчеты.
Я там просто привел пример общепринятых рассуждений которые и приводят к парадоксу.
Разумеется они не верные.
Я считаю так.
Есть два конверта, в одном

пиастров, в другом

пиастров.
Сумма денег в двух конвертах

мат.ожидание
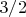
Это если я не меняю конверты.
Теперь если я меняю конверты, я либо меняю

на

, либо меняю

на

От перемены конвертов сумма денег не меняется, следовательно мат.ожидание равно по прежнему

,
другое дело, что игроку эта величина неизвестна.
А дальше уже начинаются домыслы про то, что менять выгоднее, чем не менять.
Потому что , по хорошему, считать надо выигрыш и проигрыш не от той суммы, которую я вижу, а от мат. ожидания.
Меняя конверты, я либо меняю

на

, либо наоборот.