Колесо радиусом

катится по прямолинейному пути с постоянной скоростью

без проскальзывания. Найти закон движение, а так же зависимость от времени компонент скорости и ускорения той точки колеса, которая в начальный момент времени касалась земли.
Я не очень понимаю, в чем моя ошибка.
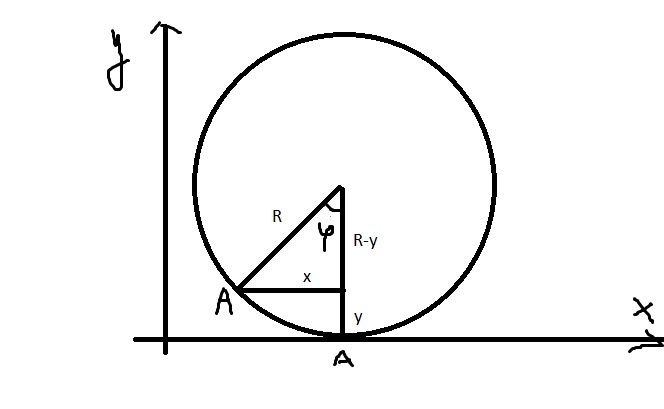
Найдем положение на оси

этой точки, когда колесо провернулось на некоторый угол

. Из рисунка видно, что

Откуда

Аналогично

Не сходится!