Уважаемые форумчане!
Помогите, плиз, разобраться в следующей задаче.
Задача: найти аргумент комплексного числа

, удовлетворяющего условию

1. Первый вариант решения - найдем

,

, полагая

, и

.
Получается следующая цепочка равенств:















Первое решение при подстановке в (5) дает неправильный результат

, второе решение тоже не подходит, т.к.

- вещественные числа. Что делать?
2. Второй вариант решения. Получается следующая цепочка:








Таким образом, если

, то

. Но тогда

и значит

. Получается, что

. Но, опять, при подстановке такого

в исходное уравнение (2.1) получаем странное равенство

. Что делать? Ясное дело, что решение
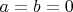
при обоих методах решений, удовлетворяют уравнению. Но аргумент комплексного числа тогда не определен. Поэтому надо искать нетривиальные решения, что у меня пока не очень получается :(