Внутри выпуклого четырехугольника

выбрана такая точка

, что
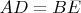
,

и

. Докажите, что

Вот рисунок сделал.

Пока что все соображения сводятся к тому, что нужно сделать неравенство треугольника тут.
Ясно, что

из неравенства треугольника. Но

, в этом проблема...