Ранее было приведено выражение, полученное из физики процесса деформации жидкого тела

где:

- средняя кривизна свободной поверхности жидкости;

- элементарное приращение площади поверхности жидкого тела при деформации;

- элементарный перемещенный объем.
Оказалось, что это же выражение легко получить, рассматривая только геометрический аспект процесса деформации жидкого тела в прямоугольном параллелепипеде. Примем, что деформация такая, что хотя бы под некоторыми ребрами контейнера образовались цилиндрические участки свободной поверхности жидкости. На одном из таких цилиндрческих участков выделим элемент поверхности единичной длины. Тогда трехмерная задача сводится к плоской, если рассматривать сечение жидкости - объем сводится к площади сечения, а площадь поверхности - к длине контура, как показано на рисунке:
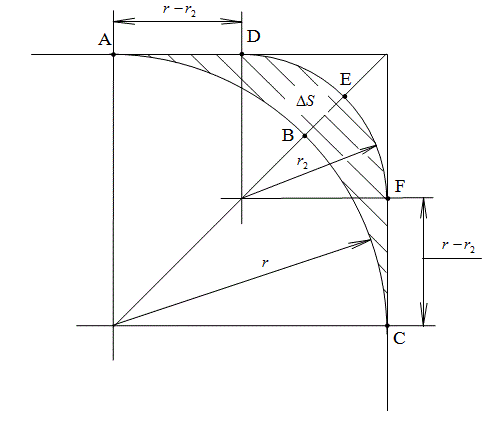
Здесь дуга радиуса

является сечением свободной поверхности жидкости в некотором состоянии деформации жидкого тела. Теперь добавим деформацию - например, чуть-чуть передвинем одну из стенок параллелепипеда, уменьшив его внутренний объем. Жидкость при этом сильнее вдавится в двугранные углы контейнера, уменьшив радиус свободной поверхности - это состояние показано дугой радиуса

. При этом заштрихованная область, площадью

, является сечением перемещенного объема жидкости, который вынудил ее свободную поверхность переместиться. Увеличение площади поверхности жидкого тела на цилиндрическом участке будет выражаться разностью:

Выразим эти величины через радиусы

и

:


Найдем отношение:

Примем

и найдем предел:

Но, как известно, средняя кривизна поверхности кругового цилиндра:

откуда получаем исходное выражение.