ДУ разрешенное относительно старшей производной

[Red_Herring]

Злые вы все. Совсем запутали бедную (включая того безобразника, что задачу поставил). Начнем с того, что задача сформулирована плохо: не сказано явно, где эти решения определены (а в этом вся соль, потому что $y_1=x$ и $y_2=\sin x$ равны только при $x=0$). Давайте добавим условие: "в окрестности $x=0$.

Munin в сообщении #879719 писал(а):

В теореме о существовании и единственности решения задачи Коши.

Совпадают ли $y_1=x$ и $y_2=\sin x$ при $x=0$?
Совпадают ли их первые производные? При каких $n \ge 1$ можно заключить, что $y_1=x$ и $y_2=\sin x$ одновременно решениями быть не могут?


К сожалению, хотя это разумно, но на всякого мудреца довольно простоты и решать эту дурацкую задачу надо по-другому.

Возьмем разные $n $.
а) Подставим $y_1=x$ в уравнение. Что получим?
б) Подставим $y_2=\sin x$ в уравнение. Что получим?
в) Возьмем разность а) и б). Каков будет порядок малости в $x=0$ левых частей (зависит от $n $)? Каков будет порядок малости в $x=0$ правых частей (не меньше чем такой же порядок для $y_1-y_2$. А он чему равен?)

ewert в сообщении #879940 писал(а):

Кстати: уравнение-то Вы угадали?...

А Вы то сами угадали? (Evil chuckling)

[tpm01]

ewert, в линейное однородное ДУ с постоянными коэффициентами вида
$y^{(n)}+a_1y^{(n-1)}+...+a_ny=0$

[ewert]

Red_Herring в сообщении #880052 писал(а):

не сказано явно, где эти решения определены

Сказано достаточно явно: правая часть -- гладкая на плоскости. И, соответственно, в окрестности нуля в т.ч.

Red_Herring в сообщении #880052 писал(а):

а) Подставим $y_1=x$ в уравнение. Что получим?

Ничего не получим, естественно. Уравнения-то нет.

tpm01 в сообщении #880060 писал(а):

в линейное однородное ДУ с постоянными коэффициентами вида
$y^{(n)}+a_1y^{(n-1)}+...+a_ny=0$

Да в какое конкретно-то?... В какие-то уравнения эти функции имеет смысл подставлять, а в какие-то -- ни малейшего.

[tpm01]

ewert, коэффициенты уравнения считаю вещественными и постоянными, при $n=1$ это уравнение 1-го порядка, подставляю $y_1=x$, уравнение будет:
$y'+a_1y=0$, после подстановки:
$1+a_1x=0$, т.к. $a_1$ постоянное и вещественное, то его подобрать невозможно, т.е. $n=1$ отпадает.
Затем принимаю $n=2$, рассматриваю следующее уравнение и т.д.
Как обосновать подобранный вид уравнения, только тем, что корни подходят?

[ewert]

tpm01 в сообщении #880062 писал(а):

Как обосновать подобранный вид уравнения, только тем, что корни подходят?

Никак не обосновать. Таким образом Вы способны лишь подобрать подходящее уравнение. Т.е. реализовать лишь первый пункт плана Vince Diesel. А насчёт второго -- слушайте Munin.

[Red_Herring]

ewert в сообщении #880061 писал(а):

Сказано достаточно явно: правая часть -- гладкая на плоскости. И, соответственно, в окрестности нуля в т.ч.

Это про правую часть сказано, а "соответственно" это Ваши домыслы.

ewert в сообщении #880061 писал(а):

Ничего не получим, естественно. Уравнения-то нет.

Я сказал "возьмем $n$". Как же нет уравнения? Да вот же оно: $y^{(n)}= f(x,y)$. Чему равна $n$-ая производная от $y_1=x$? А от $y_2=\sin x$? Ну да, зависят от $n$ но очень просто. Рассмотрим $y_1^{(n)}-y_2^{(n)}$. Какой порядок малости в $0$ (опять-таки зависит от $n$ но очень просто)?

(Оффтоп)

А задача дурацкая, потому что реально к теории ОДУ отношения не имеет. И никие Ваши хитрые планы здесь не работают в силу очень специального вида уравнения (ну нет там производных от $y$ в правой части, только $y$!)

[tpm01]

Munin в сообщении #879932 писал(а):

Окей, в этом процессе вы уже задачу Коши, и условия существования и единственности её решений проходили?

Проходила, вот до 19-й лекции включительно. Только там одни лекции без практических занятий. А вообще есть какой-нибудь задачник по этой теме, чтобы там задачки с решениями были? По типу того, что вначале условия, а в конце решения, чтобы можно было попробовать решить и свое решение сравнить с задачником. В данном курсе тесты для проверки, я их прохожу, а корректность решения они не проверяют.

[ewert]

Red_Herring в сообщении #880065 писал(а):

А задача дурацкая, потому что реально к теории ОДУ отношения не имеет.

Реально имеет, и очень принципиальное. И задачка отнюдь не дурацкая. То, что она до некоторой степени угадайка -- не очень хорошо, да; но её принципиальности это не отменяет.

Ладно, скажем открытым текстом. Почему там порядок не меньше четырёх?... -- очень просто: потому, что у этих двух функций в нуле совпадают три первых начальных условия и лишь по четвёртому они различаются.

А почему четвёрка реализуется?... -- а это ещё проще: потому, что линейные однородные дифференциальные уравнения с постоянными коэффициентами и характерные для них решения у всех на слуху.

Или, если думать в обратную сторону: если пытаться подбирать для этой пары решений подходящее ЛОДУ ПК, то очевидно, что менее чем четвёртым порядком никак не обойтись (как минимум если коэффициенты вещественны), четвёртым же можно. После чего можно уже выходить для подтверждения на теорему существования и единственности.

Так что задачка -- вполне сознательна, она задействует именно базовые знания. Недостаток лишь в том, что нужно догадаться глянуть на окрестность нуля.

[Munin]

tpm01
Можно задать дифференциальное уравнение однозначно, только если задать все его решения. А если даны только два решения - дифференциальное уравнение однозначным не будет. Можно подобрать несколько разных дифференциальных уравнения, имеющих эти два решения. Они будут отличаться где-то в других решениях.

[Red_Herring]

ewert в сообщении #880072 писал(а):

А почему четвёрка реализуется?... -- а это ещё проще: потому, что линейные однородные дифференциальные уравнения с постоянными коэффициентами и характерные для них решения у всех на слуху.

ewert, Munin

Вы читали условия задачи? Если нет, то прочтите. Если да, то зачем tpm01 лапшу на уши вешаете? Правая часть не включает в себя никаких производных от $y$, только саму функцию. Возможно, что имелось в виду что-то другое, но я не ясновидящий. Да и "на всей плоскости" ...

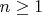
Заметим, что $y_1^{(n)}-y_2^{(n)}$ в зависимости от $n$ будет либо $1-\cos (x)$, либо $\pm \sin (x)$, либо $\pm \cos (x)$, т.е. имеет ноль порядка в точности 2, 1, 0. В то же время $|f(x,y_1(x))-f(x,y_2(x))|\le L |y_1(x)-y_2(x)|= L |x-\sin (x)|$ имеет ноль порядка 3, а то и выше. Поэтому ни при каком $n\ge 1$ такого уравнения не существует.

Если же автор имел в виду $n=0$, то да, "уравнение" $y=y $ формально правильно, а по существу издевательство (© ВИЛ)

Ну, какое отношение всё это имеет к теории ОДУ? tpm01, скажите, пожалуйста, где Вы эту задачку взяли?

[tpm01]

Red_Herring в Интуите видео-курс "Дифференциальные уравнения", там тесты, ссылка в посте выше.

[Red_Herring]

tpm01 в сообщении #880176 писал(а):

ссылка

Ну Вы бы хотя бы указали в какой лекции… Задача, как я объяснил дурацкая. В том виде, в каком ее решали многозвездные Заслуженные Участники она бы была вполне разумной: действительно, по теореме единственности никакое уравнение вида

$$ y^{(n)} = f(x, y,\ldots, y^{(n-1)}) $$

степени меньше 4 с гладкой $f $ решений $x$ и $\sin(x)$ в окрестности 0 одновременно иметь не может; а вот линейное однородное уравнение

$$ y^{IV}=-y'' $$

имеет (а также много других более общих уравнений, например

$$ y^{IV}=-y''+ (y''+\sin (x))(y-x). $$

И неединственность примера отнюдь не недостаток. Проблема в том, что никакое из уравнений гораздо более специального вида $y^{(n)}=f(x,y)$ с гладкой $f$ решений $x$ и $\sin(x)$ в окрестности 0 одновременно иметь не может и это доказывается не из общей теории ОДУ, а путем "тупой" подстановки этих функций в уравнение и элементарных рассуждений из анализа.

Как я уже отметил, на всякого мудреца довольно простоты.

[Vince Diesel]

Red_Herring в сообщении #880065 писал(а):

А задача дурацкая, потому что реально к теории ОДУ отношения не имеет. И никие Ваши хитрые планы здесь не работают в силу очень специального вида уравнения (ну нет там производных от $y$ в правой части, только $y$!)

Да, не обратил я на это внимание Но рассуждать тогда можно с привлечением ДУ и без оценок так. Пусть существует нужная $f$ для некоторого $n$. Тогда $y(x)$ будет решением $y^{(m)}=\pm f(x,y)$ для $m$ равного либо 2 либо 3, поскольку производные синуса с точностью до знака это синус или косинус. А для таких $m$ срабатывает теорема единственности.

Мда. Случай $n=0$ под это не попадает. Надо догадываться отдельно. Если его отбросить, формулировка задачи получается провокационной, ибо ответ ни для каких А так ничего себе задача.

[Red_Herring]

Vince Diesel в сообщении #880196 писал(а):

Пусть существует нужная $f$ для некоторого $n$. Тогда $y(x)$ будет решением $y^{(m)}=\pm f(x,y)$ для $m$ равного либо 2 либо 3

Тогда $y(x)$ будет решением $y^{(m)}=\pm f(x,y)$ для $m$ равного 1, либо 2 либо 3.

[Vince Diesel]

Имел в виду "пусть для $n\ge4$..." А $n=1$ автоматом пропустил, поскольку тоже запрещено теоремой единственности.