Задача 4.8Установите следующие утверждения, считая

произвольной формулой,
а относительно

предполагая, что в нее не входит

:
(а) Первая строка истинной таблицы

состоит из t.
(b) Если

(пусть

обозначает общезначимость), то

содержит по крайней мере одно вхождение связки

.
(c) Если
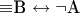
, то

содержит по крайней мере одно вхождение связки

(a) интуитивно понятно и следует из теоремы о подстановках.
С (b) и (c) не все прозрачно.