Здравствуйте. Нужна функция

, которая бы соответствовала следующим требованиям:
1.

2.

3. Имелся бы только один максимум при

и

, т.е наибольшее значение функции не должно быть ограничено сверху, например, единицей, но и не должно быть бесконечностью.
4. Хотелось бы, чтобы она выражалась только через элементарные функции.
Меня интересует эта функция при
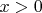
Какую функцию можете посоветовать?