Вы немного не в ту сторону идёте. Если идти с начала и не пытаться забежать вперёд, формулы будут вылезать сами как грибы, только ещё и в нужном порядке (грибы так не всегда делают).
Сначала есть радиус-векторы шаров
 *
* и скорости
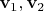
в системе отсчёта стола. Это известные величины. Теперь надо перейти в систему отсчёта центра масс (почему — ниже). Думаю, угадаю правильно, что массы всех шаров равны? Тогда радиус-вектор центра масс будет просто средним арифметическим от радиус-векторов шаров,

. Скорость центра масс найти можете? Прямо по определению скорости.
Следующий вопрос: преобразования Галилея знаете? (Думаю, что знаете, даже если не знали, что они так называются.) Найдите преобразование, переводящее центр масс в начало координат и делающее его скорость нулевой. Это преобразование свяжет положение

и скорость

любой штуки в системе отсчёта стола и положение

и скорость

в системе отсчёта центра масс шаров. Это пригодится потом.
В системе отсчёта центра масс у сталкивающихся шаров противоположные импульсы (это не с неба спустилось и показывается) до столкновения и снова противоположные, но не обязательно такие же по модулю, как были, после столкновения. Чем больше энергии переходит в тепло, тем меньше остаётся. Если в тепло ничего не переходит (это называют абсолютно упругим столкновением, но это не важно), шары обменяются импульсами. Или сменят направление импульсов — здесь всё едино, тем эта система отсчёта и хороша.
Так что считаем импульсы (а если массы шаров одинаковые, можно обходиться скоростями, конечно) в системе центра масс, меняем знаки, считаем в обратном направлении — и всё. И никаких направляющих косинусов. Зачем вам вообще углы и косинусы?
* Полужирный шрифт обозначает вектор вместо стрелки; если вам удобнее стрелки — пишите их, если вдруг понадобится.