Приведение уравнения второго порядка к каноническому виду

[Alexanderus]

Мне требуется перейти от целевой СК к канонической. Узнать углы поворота осей. А Maple я использовал для того, что бы посмотреть что должно получиться. Здесь я и хотел понять как привести мое уравнение к каноническому виду, так как у меня самого невышло.Что посоветуете сделать, что бы привести. То, что я пробовал((http://ruseti.ru/vm/stud/node82-1.html),у меня не получилось.Когда я нахожу собственные векторы у меня получаеться, что фундаментальная система решений содержит много решений(а первое равно 0, второй любому числу, третие 0). И как дальше быть?Раскажите пожалуйста поподробнее.Лучше на примере, пусть даже на другом.

[Brukvalub]

Alexanderus писал(а):

Что посоветуете сделать, что бы привести. То, что я пробовал((http://ruseti.ru/vm/stud/node82-1.html),у меня не получилось.Когда я нахожу собственные векторы у меня получаеться, что фундаментальная система решений содержит много решений(а первое равно 0, второй любому числу, третие 0). И как дальше быть?Раскажите пожалуйста поподробнее.

Даже и не знаю, что Вам присоветовать. Дело в том, что
1.После того, как Вы уточнили постановку задачи, мне стало ясно, что Вы выбрали описание именно того алгоритма, который Вам нужен. Более того, Вы нашли хорошее описание, подробное, ясное и написанное доступным языком.
2.В Вашей задаче коэффициенты квадратичной формы являются длинными десятичными дробями, возиться самому с такими коэффициентами "вручную", чтобы написать Вам решение, вряд ли кому-то захочется.
3.Вы пишете, что у Вас не получается реализовать алгоритм, с другой стороны применяемый Вами алгоритм - правильный, и всегда реализуемый.
4.Напрашивается вывод:либо Вы неправильно поняли алгоритм, либо где-то неверно его применяете. Значит, Вам нужно расписать здесь поэтапно прямо в числах и с комментариями Ваши действия, тогда, возможно, удастся найти причину Ваших затруднений.










.

[Alexanderus]

нашел лямбду. ( $\lambda=298,34$ ,$\lambda=2,160902$,$\lambda= - 0,220902$ ). Какая из них считать первой, второй,третей?Есть какая-нибудь разница?
Нахожу сообстенные векторы. Для $\lambda=298,34$

$ \left\{ \begin{array}{l} -296,6756$\alpha_1 + 0$\alpha_2$ - 0,9675$\alpha_3 = 0$,\\ 0$\alpha_1 + 0$\alpha_2$ + 0$\alpha_3 = 0$,\\ -0,9675$\alpha_1 + 0$\alpha_2$ - 298,0644$\alpha_3 = 0$, \end{array} \right. $
Видно, что
$\alpha_2 $ = любому числу.Значит можно взять и 1(тоесть берется по произволу)?
$\alpha_1 = 0?$
$\alpha_3 = 0?$
Из-за $\alpha_2$ получается, что фундаментальная система решений содержит много решений. В качестве собственного вектора можно взять
$\alpha$ = $ \left\{ \begin{array}{l} 0,\\ 1, \\ 0, \end{array} \right. $
Извиняюсь, матричного кода не нашел.

Для $\lambda=2,160902$
$ \left\{ \begin{array}{l} -0,496502$\beta_1 + 0$\beta_2$ - 0,9675$\beta_3 = 0$,\\ 0$\beta_1 + 296,179098$\beta_2$ + 0$\beta_3 = 0$,\\ -0,9675$\beta_1 + 0$\beta_2$ - 1,885302$\beta_3 = 0$, \end{array} \right. $
$\beta_2=0$
$\beta_3 = любому числу. Пусть тоже 1. Тогда
$\beta_1$ = -1, 9486325

$\beta$ = $ \left\{ \begin{array}{l} -1, 9486325,\\ 0, \\ 1, \end{array} \right. $


Для $\lambda= - 0,220902$
$ \left\{ \begin{array}{l} 1,885302$\gamma_1 + 0$\gamma_2$ - 0,9675$\gamma_3 = 0$,\\ 0$\gamma_1 + 298,560902$\gamma_2$ + 0$\gamma_3 = 0$,\\ -0,9675$\gamma_1 + 0$\gamma_2$ + 0,496502$\gamma_3 = 0$, \end{array} \right. $
$\gamma_2=0$
$\gamma_3 = любому числу. Пусть 1. Тогда
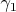
$\gamma_1$ =0,513180

$\gamma$ = $ \left\{ \begin{array}{l} 0,513180,\\ 0, \\ 1, \end{array} \right. $

( $\alpha$ , $\beta$ )=( $\alpha$ , $\gamma$)=( $\beta$ , $\gamma$)
Собственные векторы попарно ортогональны.
Их длины равны соответственно 1; 2,19024396; 1,12399.
i' = $ \left\{ \begin{array}{l} 0,\\ 0, \\ 1, \end{array} \right. $

j' = $ \left\{ \begin{array}{l} - 0,88968742,\\ 0, \\ 0,456570 \end{array} \right. $

k' = $ \left\{ \begin{array}{l} 0,4565699,\\ 0, \\ 0,88968763 \end{array} \right. $
Состаляю матрицу перехода S.(не нашел матричного кода).Здесь нет ошибки.
Старые координаты связаны с новыми уравнениями
x = 0x' - 0,88968742y' + 0,4565699 z'
y = 0x' + 0y' + 0z' = 0
z = x' + 0,456570y' + 0,88968763z'
Теперь, как я понимаю, надо подставить в это уравнение.Затем привети подобные члены.Выделить полный квадрат.
$\lambda_1*(x')^2 + \lambda_2*(y')^2+\lambda_3*(z')^2+b_1'*x'+b_2'*y'+b_3'*z' + c = 0
где b_1' = 36,549, b_2' = - 149,17, b_3' = 26,15, c = 198,33
Как определить какая лямда первая, какая вторая, какая третия?Проверьте ,пожалуйста, пока это и постарайтесь ответить на вопросы в тексте. Если есть ошибки или замечания, то пишите.

[Brukvalub]

Alexanderus писал(а):

Какая из них считать первой второй и третей?Есть какая-нибудь разница?

Разницы нет.

Alexanderus писал(а):

Нахожу сообстенные векторы для $\lambda=298,34$

$ \left\{ \begin{array}{l} -296,6756$\alpha_1 + 0$\alpha_2$+0,9675$\alpha_3 = 0$,\\ 0$\alpha_1 + 0$\alpha_2$+0$\alpha_3 = 0$, \end{array} \right. $

Здесь я вижу противоречие с теорией.
1.С одной стороны, Вы нашли три разных корня характеристического уравнения для матрицы 3х3, и тогда геометрические кратности этих корней должны быть равными 1, то есть каждое из собственных подпространств, отвечающих какому-либо корню, должно быть одномерным.
2.С другой стороны, пространство решений выписанной Вами системы для первого из корней - двумерно.
3.Вывод: где-то в Ваших вычислениях содержится ошибка. Ищите её.

Добавлено спустя 2 часа 28 минут 20 секунд:

Оказывается, Вы потом исправили свое сообщение, после чего мои замечания стали неактуальны.

[Alexanderus]

А то, что y = 0x' + 0y' + 0z' = 0 это нормально?

Добавлено спустя 21 минуту 37 секунд:

И с чем связано то что не имеет значение какая лямбда (1,2,3).Это же должно повлиять на что-то?

[Bod]

Alexanderus писал(а):

Как привести такое уравнение к каноническому виду?
$1,6644x^2 + 298,34y^2 + 0,2756z^2 -1,935xz +36,549x-149,17y + 26,15z+ 198,33 = 0$
Пытался делать как написано здесь(http://ruseti.ru/vm/stud/node82-1.html), но не получилось.Остановился на нахождении собствееных векторов(получается, что они равны 0).Известно, что должен получиться либо эллипсойд, либо конус.Помогите разобраться как это делается...

Я ради интереса посмотрел собственные вектора вашей квадратичной формы и у меня они ни как не равны нулю.
P=

\[ \begin{array}{*{20}c} {{\rm{ 0}}{\rm{.4566}}} & {0,8897} & 0 \\ 0 & 0 & { - 1} \\ { - 0,8897} & {0,4566} & 0 \\ \end{array} \]

Добавлено спустя 18 минут 59 секунд:

А на каком основании вы так получаете вектор

\[ {i'} \]

из вектора

\[ \alpha \]

??

[Alexanderus]

Тьфу. вот она ошибка. Спасибо, Bod. Теперь должен получиться конус! Я только не понял, почему не имеет значение какая лямбда первая, какая вторая, ну и третия?

[Brukvalub]

Alexanderus писал(а):

' = $ \left\{ \begin{array}{l} 0,\\ 0, \\ 1, \end{array} \right. $

j' = $ \left\{ \begin{array}{l} - 0,88968742,\\ 0, \\ 0,456570 \end{array} \right. $

k' = $ \left\{ \begin{array}{l} 0,4565699,\\ 0, \\ 0,88968763 \end{array} \right. $

Что это за вектора? Как они получены?

[Alexanderus]

i' = (1/|&\alpha$|)*&\alpha$

[Brukvalub]

Меня, как и Bodа сбил с толку первый вектор, но теперь Вы и сами увидели, что ошиблись. Двигайтесь дальше.

[Bod]

Цитата:

Я только не понял, почему не имеет значение какая лямбда первая, какая вторая, ну и третия?

Это просто в дальнейшем определит номер собственного вектора и при построении матрицы для перехода к другому базису лишь изменит порядок собственных векторов, то есть вы в любом случае получите канонический вид, просто последовательность записи будет той или иной.

[Alexanderus]

$$\frac {(x'-0.25)^2} {1,58965239} + \frac {(y' +46,57694365)^2} {2146,91082} - \frac{(z'+9,24404605)^2} {219,47172713} = -1 $$

Реультат поразительный!Получился двухполосный гиперболойд, хотя в задание было сказано, что должен получиться либо эллипсойд, либо конус. Методом Лагранжа тоже получился двухполосный гиперболойд! А углы поворота осей как-нибудь можно найти, зная каноническое уравнение?
Коэффициет С=198.33 в исходном уравнение влияет на получение конуса/двухполосного гиперболойда?Я так понимаю, что только при одном значение С может получиться конус.Я прав?

[Brukvalub]

Alexanderus писал(а):

А углы поворота осей как-нибудь можно найти, зная каноническое уравнение?

Чтобы найти углы поворота осей, нужно знать координаты базисных векторов того базиса, в котором форма имеет канонический вид, относительно исходного базиса.

Alexanderus писал(а):

Коэффициет С=198.33 в исходном уравнение влияет на получение конуса/двухполосного гиперболойда?Я так понимаю, что только при одном значение С может получиться конус.Я прав?

Не прав.

[Alexanderus]

Значит, для одного уравнения может быть несколько значений С ,при которых получается конус?

[Brukvalub]

Да. Например:

\[x^2 - y^2 + cz^2 = 0\]

. При с=1 и при с= - 1 получается конус.