Теория вероятности, гауссовский вектор

[ejk]

svv

Т.е. получается, что у нас еще и у каждой случайной величины,которая входит в вектор разные параметры распределения? Ничего себе.

[svv]

Так это же вполне укладывается в способ описания. Даже матрица ковариации только и ждет, чтобы для каждой из с.в. — компонент вектора Вы задали свою дисперсию и вписали в соотстветствующую ячейку.

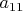
Представьте, есть вектор из двух непрерывных случайных величин $X_1$ и $X_2$, одинаково распределенных и независимых. Дисперсии у них, понятно, одинаковы: $a_{11}=a_{22}$. Теперь я первую компоненту вектора $X_1$ умножаю на $5$. Линейное такое преобразование. Дисперсия, т.е. элемент $a_{11}$ в матрице ковариации, умножится на $25$. А элемент $a_{22}$ так и останется.

[ejk]

svv

Немного не поняла суть примера Т.е. даже если они буду независимы, у них все равно будут разные параметры распределения или что?

[svv]

Суть в том, что из законного (в Вашем смысле) примера с одинаковыми дисперсиями я законными действиями получаю разные дисперсии. Следовательно, такая ситуация тоже законна.

[ejk]

svv

То бишь нужно рассматривать общий случай, когда ничего ничему не равно, так?

[svv]

Вы можете быть уверены, что матрица $A$ симметричная и положительно полуопределенная. Первое означает, что $a_{12}=a_{21}$, второе — это некоторые неравенства.

[ejk]

svv в сообщении #831785 писал(а):

Требуем, чтобы это обращалось в нуль. С учетом $a_{12}=a_{21}$ получаем $\tg 2\varphi=\frac{2a_{12}}{a_{11}-a_{22}}$.

Дальше Вы.

Т.е. остается выразить угол, а потом сказать, что в общем виде нужна матрица выглядит так-то, а угол будет такой-то?

[svv]

Так как в матрице $S$ присутствует не сам угол, а только $\sin\varphi$ и $\cos\varphi$, то нахождение самого $\varphi$ как арктангенса будет малополезным. В ответе желательно выразить $\sin\varphi$ и $\cos\varphi$ через элементы матрицы $A$ и про угол уже не упоминать.

[ejk]

svv

А там же когда мы выражение это преобразуем(которое приравняли к нулю), то получается квадратное уравнение относительно тангенса, так ведь? А откуда потом появляется тангенс двойного угла?

[svv]

Вот подробно:
$a'_{12}=(a_{22}-a_{11})\cos\varphi\sin\varphi+a_{12}\cos^2\varphi-a_{21}\sin^2\varphi=0$

$a_{12}(\cos^2\varphi-\sin^2\varphi)=(a_{11}-a_{22})\cos\varphi\sin\varphi$

$\dfrac{a_{12}}{a_{11}-a_{22}}=\dfrac{\sin\varphi\;\cos\varphi}{\cos^2\varphi-\sin^2\varphi}$

В числителе $\frac 1 2\sin 2\varphi$, в знаменателе $\cos 2\varphi$. Так и получается тангенс двойного угла. Но если Вы считаете, что такое преобразование нецелесообразно, можно это и не делать.

[ejk]

И получается одно равенство на два неизвестных...

[svv]

Так они же связаны, $\sin^2\varphi+\cos^2\varphi=1$.

[ejk]

У меня получилось уравнение 4й степени для синуса. Это нормально?

$(4a_{12}^2+(a_{11}-a{22})^2)\sin^4{\varphi}-(4a_{12}^2-(a_{11}-a_{22})^2)\sin^2{\varphi}+a_{12}^2$

[svv]

Достаточно написать
$\begin{pmatrix}\eta_1\\\eta_2\end{pmatrix}=\begin{pmatrix}\cos\varphi&\sin\varphi\\-\sin\varphi&\cos\varphi\end{pmatrix}\begin{pmatrix}\xi_1\\\xi_2\end{pmatrix}$, где $\tg 2\varphi=\dfrac{2a_{12}}{a_{11}-a_{22}}$.
На всякий случай: здесь матрица $S^{-1}$, она отличается от $S$ знаком $\varphi$ (и, в результате, знаками при синусах).

Если нужны явные формулы, можно так. Обозначим
$k=\dfrac{2 a_{12}}{a_{22}-a_{11}}\quad s=\sin\varphi\quad c=\cos\varphi$

Тогда $k=\dfrac{2sc}{c^2-s^2}$.
Возводим в квадрат, выражаем косинус через синус:
$k^2(1-2s^2)^2=4s^2(1-s^2)$
$(2s^2-1)^2=\frac 1 {1+k^2}$

$s^2=\frac 1 2(1\pm\frac 1{\sqrt{1+k^2}})$
$c^2=\frac 1 2(1\mp\frac 1{\sqrt{1+k^2}})$

[ejk]

svv

А почему в минус первой степени? Она же у нас и должна справа, чтобы преобразовать исходный вектор.