Попробуйте в качестве оператора взять проекцию. Скажем, на плоскость, параллельно некоторому вектору. Даже просто проекцию на плоскость

параллельно оси

.
Все равно не понял, где здесь факторпространство и где ядро. Приведите, пожалуйста, примеры и укажите, где там фактор-пространство и где ядро. Может до меня дойдет тогда.
Давайте не так.
Приведите сами какие-нибудь примеры линейных функционалов из геометрии, а мы поможем с ядрами (и этими ужасными факторпространствами)
Евклидова норма трехмерных векторов.
Вот читаю у Колмогорова (да и в десятке другом книг). Привожу, чуть вырезав.
Цитата:
Пусть

-линейное пространство, а

-некоторое его подпространство. Два элемента

и

из

эквивалентны, если их разность

принадлежит

. Это отношение разбивает все

из

на классы. Класс эквивалентных элементов называется классом смежности (по подпространству

). Совокупность всех таких классов называется фактор-пространством

по подпространству

.
Рассуждаю.
Как примеры подпространств трехмерного пространства могу привести: плоскости, отрезки, больше в голову не приходит (может дадите еще примеров). Вот нарисовал как разность одной пары векторов и разность другой пары векторов лежат в одной плоскости(которая есть подпространство трехмерки):
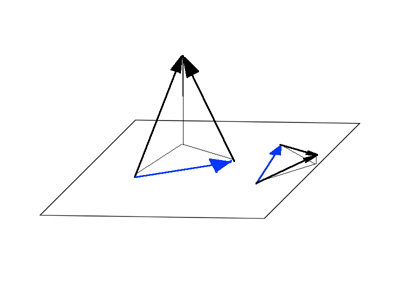
Есть вектора, разности которых лежит в других плоскостях. Для каждой плоскости имеем свой класс векторов, разность которых лежит в ней. Дальше я не понимаю, где здесь фактор-пространство.
Теперь функционал (опущу "линейный" для краткости).
Цитата:
Назовем ядром

произвольного множества

совокупность таких его точек

, что для каждого

найдется такое число

, что

при

. Выпуклое множество, ядро которого не пусто, называется выпуклым телом. В трехмерном Евклидовом пространстве куб, шар, тетраэдр представляют собой выпуклые тела.
Для примера куба в трехмерном пространстве,

-трехмерное пространство,

-сам куб.

- в общем случае точка трехмерного пространства, которая не обязана быть внутри или на границе куба, но может быть вне его. Что такое

, я не могу представить.