Сущ-ет сколь угодно длинное бесквадратное слово из 3-х букв

[Sonic86]

Дан алфавит $A=\{a,b,c\}$. Надо доказать, что в этом алфавите можно написать сколь угодно длинное слово $W$, не содержащее квадратов (т.е. такое, что уравнение $W=AB^2C$ не имеет решений при $B\neq\varepsilon$ в полугруппе $\langle a,b,c\rangle$).
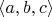
Пытался явно строить такое слово - не вышло.
Пытался строить какие-то итеративные тройки слов - тоже не получается.
Сейчас пытаюсь найти рекуррентную формулу. Получается что-то вроде $t_{n+1}=(3-1)t_n-\sum\limits_{2k<n}t_{2k}$, но еще не проверил.
Последовательность в OEIS нашел, но сильно не помогло.
В общем, плохо получается.
Есть простое решение?

[patzer2097]

Один из простейших примеров бесконечного бесквадратного слова над алфавитом из 3 букв можно построить, если начать с слова w_1=a и далее из слова w_i получать слово w_{i+1} с помощью замен «a»->«abcab», «b»->«acabcb», «c»->«acbcacb». Это из Википедии, может, это поможет как-то...

[Deggial]

patzer2097 в сообщении #805325 писал(а):

Один из простейших примеров бесконечного бесквадратного слова над алфавитом из 3 букв можно построить, если начать с слова w_1=a и далее из слова w_i получать слово w_{i+1} с помощью замен «a»->«abcab», «b»->«acabcb», «c»->«acbcacb».

patzer2097, замечание за неоформление формул $\TeX$ом