Помогите решить 2 геометрических задачи

[Бек]

незваный гость
[quote] Вы имееие ввиду этто иесть решение задачи если да то я чо то не врубаюсь откуда эти цифры.
В этой задаче не будем принимать во внимание этот треугольник(равносторонний) т.к. определить прямую не получится т.к. мы можем ее провести как угодно=> мы не будем принимать во внимание правильные треугольники т.е. я имея ввиду что берется произвольный остроугольный треугольник.

[незваный гость]

Бек писал(а):

В этой задаче не будем принимать во внимание этот треугольник(равносторонний) т.к. определить прямую не получится

А нам не надо определять прямую. Нам достаточно того, что она существует.

Бек писал(а):

Вы имееие ввиду этто иесть решение задачи если да то я чо то не врубаюсь откуда эти цифры.

А Вы проверить (решение это или нет) не можете? Тогда — плохо.

А откуда … главное, что они на заданный Вами вопрос отвечают.

[незваный гость]

Бек писал(а):

2.условие тоже самое толька сще проведены медианы.образуется 3 точки можетли так быть что образуется равносторонний треугольник

Если не проврался в расчетах, точки пересечения биссектрис, медиан и высот никогда не образуют равносторонний треугольник.

[Батороев]

Имеем треугольник $ ABC $
Углы при вершинах обозначим соответственно $ \alpha, \beta, \gamma $.
Из вершин $ A $ и $ C $ проведем высоты.
Угол между высотой, проведенной из вершины $ A $, и стороной $ AC $ равен:
$ x = \frac{\pi}{2} - \gamma $
Угол между высотой, проведенной из вершины $ C $, и стороной $ AC $ равен:
$ z = \frac{\pi}{2} - \alpha $.
Радиус вписанной окружности $ r $.
Длина стороны $ AC $ равна $ a $.

Допустим, что линия, соединяющая центр вписанной окружности (цво) и точку пересечения указанных высот (тпв), параллельна $ AC $.
Тогда $ a $ можно выразить двумя способами:
$ a = r\ctg{\frac{\alpha}{2}} + r\ctg{\frac{\gamma}{2}} $
$ a = r\ctg x + r\ctg z = r\ctg{(\frac{\pi}{2}} - \alpha) + r\ctg{(\frac{\pi}{2} - \gamma)} $.

Уравняв эти выражения и сократив на $ r $, получаем:
$ \ctg{\frac{\alpha}{2}} + \ctg{\frac{\gamma}{2}} = \ctg{(\frac{\pi}{2}} - \alpha) + \ctg{(\frac{\pi}{2} - \gamma)} $.
Из этого уравнения, по-видимому (тригонометрию, к сожалению, подзабыл), можно найти соотношение между углами.

[Бек]

Мы еще не доказали что прямая может быть параллельна

[Батороев]

Бек писал(а):

Мы еще не доказали что прямая может быть параллельна

Как раз и решив предлагаемое уравнение, можно узнать, существуют ли другие решения
кроме тривиального $ \alpha = \beta = \gamma = \frac{\pi}{3} $ (которое также удовлетворяет условиям данного уравнения).

Кроме параллельности рассматриваемой прямой стороне треугольника $ AC $,
также необходимо рассмотреть возможность ее параллельности сторонам $ AB $ и $ BC $.

[Бек]

Именно. Но я хочу геометрическое решение

Добавлено спустя 1 минуту 4 секунды:

и еще стороны этого треугольника

[незваный гость]

Бек писал(а):

Но я хочу геометрическое решение

Сочувствую.

Бек писал(а):

и еще стороны этого треугольника

Посмотрите выше.

Lion писал(а):

Непонятно, какой стороне должна быть параллельна прямая в задаче 1.

Батороев писал(а):

Кроме параллельности рассматриваемой прямой стороне треугольника $ AC $, также необходимо рассмотреть возможность ее параллельности сторонам $ AB $ и $ BC $.

Бек писал(а):

Именно

На самом деле, поскольку ортоцентр и центр вписанной окружности определены симметрично относительно сторон, то столь же симметрично определена и прямая. Id est достаточно рассмотреть параллельность одной из сторон.

~~~~~~

Бек, если Вас действительно интересует задача, разберитесь с уже помещенной в теме информацией. Разберитесь, откуда берется расстояние от ортоцентра до стороны, как работает неконструктивное доказательство существования, и можно ли его упростить.

Выскажу еще одно утверждение:

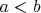
Для любых двух отрезков $a$ и $b$, $a < b$ существует и притом единственный отрезок $b < c < \frac{21}{20} b$, такой, что в треугольнике со сторонами $a$, $b$, $c$ прямая, проходящая через точки пересечения биссектрис и высот, параллельна одной из сторон треугольника. Более того, это всегда $b$.

Несколько замечаний о свойствах этого чуда-юда $c$: 1) для рациональных $a, b$ оно всегда иррационально, 2) его невозможно построить геометрически, 3) верхняя граница — неточная (и, я думаю, точная граница невыразима в радикалах).

[ins-]

Please check the following solutions

Problem 1 - Solution:

Prove easily that $ IH\parallel BC \Longrightarrow $ the projection of A on BC belongs to (BC)\ !
Thus, $ \boxed {IH\parallel BC} \Longleftrightarrow \frac {2p}{a} = \tan B\tan C \Longleftrightarrow a\sin B\sin C = 2p\cos B\cos C \Longleftrightarrow abc = 8R^2p\cos B\cos C \Longleftrightarrow 4Rpr = 8R^2p\cos B\cos C \Longleftrightarrow \frac rR = 2\cos B\cos C \Longleftrightarrow \frac rR = \cos (B - C) - \cos A \Longleftrightarrow 2\cos A + \cos B + \cos C = 1 + \cos (B - C) \Longleftrightarrow \cos^2\frac A2 - \sin^2\frac A2 + \cos\frac {B + C}{2}\cos\frac {B - C}{2} = \cos^2\frac {B - C}{2} \Longleftrightarrow \sin^2\frac {B + C}{2} - \cos^2\frac {B + C}{2} = 2\sin\frac B2\sin\frac C2\cos\frac {B - C}{2} \Longleftrightarrow \left(\tan\frac B2 + \tan\frac C2\right)^2 - \left(1 - \tan\frac B2\tan\frac C2\right)^2 = 2\tan \frac B2\tan\frac C2\left(1 + \tan\frac B2\tan\frac C2\right) \Longleftrightarrow \boxed {\left(\tan\frac B2 + \tan\frac C2\right)^2 = 1 + 3\tan^2\frac B2\tan^2\frac C2}\ .$ Denote $ \tan\frac B2 = x, \tan\frac C2 = y\ $.
Thus, $ IH\parallel BC \Longleftrightarrow$ exist $ x > 0, y > 0 $ so that $ (x + y)^2 = 1 + 3x^2y^2 $, i.e. exists x > 0 so that the equation (in y)
(3x^2 - 1)\cdot y^2 - 2x\cdot y + 1 - x^2 = 0 $ has at least a positive root. It is possibly, for example $ \frac {\sqrt 3}{3} < x < 1$ !

$ \boxed{IH\|BC}\Longleftrightarrow (b + c).tgA = (tgB + tgC).a\Longleftrightarrow \\ \Longleftrightarrow (b + c).\frac {tgB + tgC}{1 - tgB.tgC} + (tgB + tgC).a = 0\Longleftrightarrow tgB.tgC = \frac {a + b + c}{a} = \frac {h_a}{r} $.

Using the sin and cos laws, have: $ \\ (b+c).tgA=a.(tgB+tgC)\Longleftrightarrow (b+c).\frac{sinA}{cosA}=a.(\frac{sinB}{cosB}+\frac{sinC}{cosC})\Longleftrightarrow \\ \Longleftrightarrow \dots \Longleftrightarrow \frac{b+c}{b^2+c^2-a^2}=a.(\frac{1}{a^2+c^2-b^2}+\frac{1}{a^2+b^2-c^2})\Longleftrightarrow \\ \Longleftrightarrow \boxed{2.a^3.(b^2+c^2-a^2)=(b+c).(a^2+c^2-b^2).(a^2+b^2-c^2)}. $

So the conclusion is there are infinitely many triangles with the desired property.


Problem 2 - Solution:
The relations $ \left\|\begin{array}{c} 9\cdot GI^2 = p^2 + 5r^2 - 16Rr \\ HI^2 = 4R^2 + 4Rr + 3r^2 - p^2 \\ 9\cdot GH^2 = 36\cdot R^2 - 8\cdot \left(p^2 - r^2 - 4Rr\right)\end{array}\right\| $ are well-known.

Therefore, $ GI = HI = GH \Longleftrightarrow \left\|\begin{array}{c} 5p^2 = 18R^2 + 26Rr + 11r^2 \\ 3p^2 = 12R^2 + r^2 + 16Rr\end{array}\right\| \Longleftrightarrow \left\|\begin{array}{c} p^2 = 3\cdot\left(2R^2 + 2Rr - 3r^2\right) \\ 3R^2 + Rr - 14r^2 = 0\end{array}\right\| \Longleftrightarrow \left\|\begin{array}{c} R = 2r \\ p = 3r\sqrt 3\end{array}\right\| \Longleftrightarrow a = b = c\ . $

In conclusion, $ \triangle\ GHI $ is equilateral iff $ \triangle\ ABC $ is equilateral, i.e. $ G\equiv H\equiv I\ $.

[нг]

ins-
Please fix your post putting $ signs around formulae only. Also, avoid placing big bodies of text inside tag [mаth].

It is next to impossible to read it as is.

[ins-]

I believe it is now better ... there is lots of things to desire ... but I'm not good in tex.
Are the solutions 'OK'?

[незваный гость]

ins- писал(а):

Are the solutions 'OK'?

Sorry, I am running out of time. I will try to check them a little later.

But a connoisseur like you might appreciate a few facts (prove them ):

(1) $|HI| \leq |GH|$, and the equality realizes in equilateral triangle only . Therefore, all other distances are irrelevant (except to simplification of solutions).

(2) Similar $|GI| \leq |GH|$, and the equality realizes in equilateral triangle only.

(3) The angle ${\scriptstyle \angle}GIH$ is always obtuse. Indeed, previous two are immediate consequence of this one.

[ins-]

That angle GIH is obtuse is very interesting result. It were easier for me to prove 1) and 2) by algebra and/or trygonometry only.
It is a complete proof. Why to reinvent the wheel when I reinvented it 5-6 times. http://www.mathlinks.ro/Forum/viewtopic.php?t=39447. If I should say the truth ... I had no chances ... I don't know vectors ... and I cannot make good constructions.

Another approach is to use some of the following inequalies http://www.mathlinks.ro/Forum/viewtopic ... 6&t=164095, cosine law and my equalities for IG, GH, HI. Or it doesn't works ... brute force.

[незваный гость]

ins- писал(а):

Problem 1 - Solution:

The first part looks correct. I cannot tell for sure as you are using implicitly equivalences I am not aware of.

The second part (after “for example $ \frac {\sqrt 3}{3} < x < 1$ ! ”) looks unrelated to the question. You get an equation involving sides, which proves exactly nothing, because there is no proof that there exist $a, b, c$ satisfying it.

ins- писал(а):

Problem 2 - Solution:

Looks correct again. But it is superseded by obtuseness of the triangle.

[ins-]

The part with interval abour x proves that there exists infinitely many such triangles. Unrelated part comes to show exact relation between sides. It proves indeed very interesting result - there exists infinitely many triples of positive of numbers - that are solutions of the given equation with properties: a+b>c, b+c>a, c+a>b.