Решение СЛАУ по методу Якоби

[rct07]

Посмотрите, пожалуйста, у меня в решении где-то ошибка.
Дано: решить систему уравнений методом Якоби: $ \left( \begin{array}{cc} 4 & 3 \\ 11 & 8 \end{array} \right)$ $ \left( \begin{array}{cc} x_1 \\ x_2 \end{array} \right)$ $ \left( \begin{array}{cc} 5 \\ 7 \end{array} \right)$.
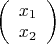
Значит, делаем так: приводим систему уравнений к виду
4\cdot x_1 +3\cdot x_2=5
11\cdot x_1 +8\cdot x_2=7
Выражаем из первого уравнения x1, из второго x2:
x_1=1.25-0.75\cdot x_2
x_2=0.875-1.375\cdot x_1
В качестве нулевого приближения примем элементы столбца свободных членов: x(0)=$ \left( \begin{array}{cc} 5 \\ 7 \end{array} \right)$
И тогда при первой итерации в первое уравнение подставляем 7 вместо x2, а во второе 5 вместо x1, так? Ну а при последующих итерациях вместо иксов подставляем значения, которые получились в предыдущих?
Фигня у меня какая-то получается. Помогите, пожалуйста.

[provincialka]

А вы условие сходимости метода проверяли? Отображение-то у вас не сжимающее! Коэффициент больше 1.

[rct07]

И что делать в таком случае?

-- 16.12.2013, 17:41 --

По достаточному признаку сходимости во второй строке диагональный элемент по модулю меньше суммы модулей остальных элементов. Как тогда преобразовать систему?

[provincialka]

Посмотрите теорию. Вы самодеятельностью занимаетесь.

[cool.phenon]

Линейными преобразованиями можно свести систему к такой, в которой будет диагональное доминирование, а корни будут такими же, как и у начальной.

[rct07]

Значит, надо её привести к диагональному виду? У меня получилось вот что: $\small \begin{pmatrix} 4 & 3 \\ 0 & -0.25 \end{pmatrix} \small \begin{pmatrix} 5 \\ -23/4 \end{pmatrix}$, это правильно? Тогда надо дальше выразить из каждого уравнения переменную, сделать матрицу вида $x=\alpha x+\beta$, где $\alpha=\small \begin{pmatrix} 0 & -a_{1,2}/a_{1,1} \\ - a_{2,1}/a_{2,2} & 0 \end{pmatrix}$ $ \beta=\small \begin{pmatrix} b_{1}/a_{1,1} \\ b_{2}/a_{2,2} \end{pmatrix}$, а дальше - итерационный процесс?

[Pphantom]

rct07 в сообщении #870345 писал(а):

Значит, надо её привести к диагональному виду?

К виду, для которого будет верно условие диагонального преобладания (доминирования). Если Вы диагонализируете матрицу, то после этого никакой итерационный процесс уже не понадобится.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Оформите все формулы в полном соответствии с topic183.html

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.