mynameНе знаю, подойдет ли к "Вопросам преподавания"... Многое я сейчас не обсуждаю, чтобы совсем в сторону не уйти. Если интересно, спросите.
Я попробую описать основные идеи квантовой механики максимально просто (благо они очень простые) Попробуйте забыть на время про всякие частицы и прочее, мой пример будет достаточно абстрактен, в то же время применим для очень многих случаев
Половина всей квантовости заключается в том, что состояние системы описывается вектором состояния. В каком смысле вектором? Пусть наша система может находиться в двух состояниях, которые я обозначу

и

. Тогда в квантовой теории в качестве состояния можно рассматривать любую линейную комбинацию этих состояний, т.е.

Где

и

- произвольные комплексные числа. Ограничимся пока только такими состояниями.
Можете представить пространство как плоскость с осями

и

. Единичные вектора вдоль осей

и

- аналоги наших

и

, а любое состояние - вектор из начала координат в какую-то точку на плоскости. Вообще все что ниже допускает такую аналогию с поправкой, что задействованы комплексные числа.
Будем считать дальше, что

. Состояния

и

образуют базис, т.е. любое другое состояние может быть записано в виде их линейной комбинации. Также как любой вектор на плоскости может быть разложен по единичным векторам вдоль осей

и

. Мы могли бы выбрать другой базис, например

На этих векторах вводится скалярное произведение

которое часто обозначается как

. Как и в школьной геометрии оно симметричное и билинейное, но из-за того, что фигурируют комплексные числа в некоторых местах выскакивает комплесное сопряжение.


Будем считать, что наш исходный базис ортонормированный

Тогда в векторе

коэффициенты разложения можно записать как скалярные произведения

Точно также коэффициенты разложения вектора на плоскости по единичным векторам вдоль осей (т.е. его координаты) запишутся как скалярные произведения с этими самыми векторами.
С другой стороны, мы можем разложить и по другому базису с коэффициентами

Теперь зачем все эти скалярные произведения нужны. Дело в том, что они связаны с вероятностями измерений. Допустим я меряю круговую поляризацию фотона и

обозначает левую круговую поляризацию, а

- правую. Тогда если фотон находится в состоянии

вероятность, что эксперимент даст левую спиральную поляризацию оказывается равной

.
Состояние системы после измерения. В самом-самом простейшем случае если мы меряем результат соответствующий

, то на выходе и получаем

. Если же меряем результат соответствующей

, то на выходе получаем

. Получаем в том смысле, что последующие эксперименты дают результат, словно произошла такая обрубка. Это и есть "коллапс волновой функции".
Но если мы меряем что-то другое, например линейную поляризацию вдоль одной из осей, то состояния имеющие определенные значения этой новой наблюдаемой может соответствовать совсем другому базису, например

и

. Измерение будет срабатывать тем же способом - проецировать на одно из базисных состояний с какой-то вероятностей.
Но к чему это ведет. Летит допустим состояние с левой круговой поляризацией

мы меряем его линейную поляризацию и в итоге получаю например

. Но это означает, что если после этого я померяю круговую поляризацию я в половине случаев померяю левую, а в половине правую и не могу сказать заранее какую из них, т.е. такое состояние не будет иметь определенной круговой поляризации.
Точно также в КМ для частиц существуют состояния с определенными координатами и определенными импульсами, но не одновременно, что и есть источник соотношения неопределенностей. И здесь я хочу отметить следующее: при измерении не происходит того, что у нас в каком-то месте выскакивает маленький упругий шарик. У нас нет оснований считать, что квантовая система не остается квантовой всегда. Просто ее состояние рубится до некоторого другого и надо сказать, что этот процесс не описывается в рамках квантовой теории замкнутых систем. На том, почему и что творится когда мы уходим от замкнутости (которая при измерении естественно нарушается) я сейчас останавливаться не буду.
Если у нас есть две не взаимодействующие системы, например две частицы на большом расстоянии друг от друга, то их состояние можно описать с помощью так называемого тензорного произведения. Пусть первая частица точно находится в состоянии

, а вторая в

. Такое состояние нашей большой системы запишем как

. Дальше скажем, что тензорное произведение билинейно, т.е.

И тут мы приходим собственно к спутанным состояниям. Дело в том, что если мы позволим линейной комбинации любых состояний быть тоже состоянием, мы допускаем и состояния вроде

которые не представимы в виде

. Такие состояния и называются спутанными. В частности то, что я написал - состояние мысленного эксперимента ЭПР и реальных экспериментов по проверке неравенств Белла.
Измерения также в принципе рубят наше состояние через проекцию на подпространство с определенным значением наблюдаемой, например если есть два спутанных фотона в состоянии

и мы меряем поляризацию первого, то если мы меряем левую поляризацию, состояние рубится до

и до

, если правую.
Так что частицы в таком состоянии нельзя описать по отдельности с помощью чистого квантового состояния. Если мы хотим забыть про вторую частицу мы сможем описать первую только с помощью так называемого смешанного состояния, для чего придется вводить матрицу плотности, чего я делать сейчас не буду. Смысл состоит в следующем - это одно из чистых состояний с какой-то вероятностью в классическом смысле (т.е. не зависящем от измерений).
Из-за вероятностного характера измерений, наблюдая за частицей по отдельности мы не видим ничего удивительного. Какая разница, спутана ли наша частица с другой, или кто-то шлет с какой-то вероятностью частицу в каком-то состояниях. Но если кто-то делает эксперименты с другой частицей, мы можем сравнить наши результаты. Что мы обнаружим это корреляции, которые невозможно описать, если считать будто за всей нашей вероятностной квантовой моделью прячется чисто классический мир с неизвестными нам скрытыми параметрами. Единственное спасение такой точки зрения - считать, что наши частицы связаны друг с другом неким сверхсветовым каналом. С другой стороны квантовая теория НЕ требует сверхсветовых сигналов и при этом прекрасно описывает эти корреляции за счет простых вещей, которые я написал выше.
-- 16.10.2013, 00:41 --Теперь простой пример эксперимента со спутанными состояниями - квантовый ластик
Два фотона разлетаются в ЭПР-состоянии. Первый фотон прилетает на двухщелевой эксперимент. На каждой из щелей стоит фильтр, который отсекает одну из поляризаций, т.е.

пролетает например через левую щель, а

через правую, поэтому переобозначим их как

и

соответственно. Т.е. состояние

Формализм матрицы плотности, который я только упомянул, дает, что если забыть про вторую частицу, на первый детектор прилетает в половине случаев

, а в половине

. Т.е. на экране за двойной щелью у нас нет интерфенции, что и показывает эксперимент. Набираем статистику - картина складывается так, что фотон проходит через каждую из двух щелей по отдельности.
Займемся вторым фотоном. Его состояния с круговой поляризацией можно разложить на состояния с линейной поляризацией, например так

Тогда наше состояние представляется в виде

Теперь если мы будем набирать статистику только для тех первых фотонов, для которых второй в состоянии
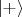
, мы получим интерференционную картину от

. Потому эксперимент называется "квантовый ластик" - в новом базисе "стирается" информация о том, через какую щель проходит фотон. С другой стороны, если набирать статистику только для тех, для которых измерения второго дают
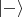
, мы получим интерференционную картину в противофазе, от

.
Если не знать, в какой именно поляризации получается второй фотон, эти две картины складываются вместе и получается картина от фотонов проходящих через две щели по отдельности.
-- 16.10.2013, 00:43 --Прочитав это вы можете придумать любое спутанное состояние из трех и более частиц. Например

Как придумаете, то можно будет заняться и исходными вопросами

Кстати, забыл упомянуть. Формулы для вероятностей написаны при условии, что вектор состояния нормирован на единицу, т.е.

, грубо говоря, единичной длины. Иначе надо поделить на квадрат его нормы - она имеет смысл "полная вероятность померять хоть что-нибудь"
-- 16.10.2013, 01:06 --Еще мелочь про квантовый ластик.
Я сказал, что в 50% случаев первый фотон прилетает в состоянии

, а в 50% случаев прилетает в

. Но с другой точки зрения (что получается во втором случае) в 50% случаев прилетает в

, а в 50% случаев прилетает в

Так вот. Это совершенно неотличимые с точки зрения наблюдений ситуации. Опять же, спасибо (или "да будет проклят", если вам хочется сверхсветовой коммуникатор) вероятностному характеру измерений