Эквивалентность множеств функций

[Mysterious Light]

Можете считать, что $f:X\to Y$ означает $f\in Y^X$, а $f: X\mapsto Y$ является сокращением для $f = \{ (X,Y) | X\in {\rm dom} f \}$, если под функцией понимать специальный вид бинарного отношения, т.е. $f\subset {\rm dom} f\times {\rm rng} f}$.
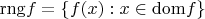
То, что Вы написали в конце ${\rm rng} f = \{ f(x) : x\in {\rm dom}f\}$ (под rng имеется в виду область значений, да?) соответствует понятию сюръекции, которое, бывает, обозначается $f:\xymatrix{A\ar@{->>}[r]&B}$.

Очевидно, для любой функции $f: x\mapsto f(x)$.
Предлагается рассмотреть:
$F(\phi) : (b,c) \mapsto \phi(b)(c)$, или по-другому $F : \phi \mapsto ((b,c) \mapsto \phi(b)(c))$.
$G(\psi) : b \mapsto (c \mapsto \psi(b,c))$, или по-другому $G : \psi \mapsto (b \mapsto (c \mapsto \psi(b,c)))$

[Manticore]

Mysterious Light
Огромнейшее спасибо! Теперь разобрался!