Athens, Greece. Время на задачи - 5 часов.
Задача 1. Найдите все непрерывные функции
![$f:[1, 8]\rightarrow\mathbb R$ $f:[1, 8]\rightarrow\mathbb R$](https://dxdy-01.korotkov.co.uk/f/0/4/5/0450ab5bf8ea78ac662130be0ba8b45382.png)
такие что

Задача 2. Пусть
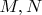
- 2 матрицы размера 2 на 2 с комплексными коэффициентами, такие что

. Докажите, что существует обратимая матрица с комплексными коэффициентами

, такая, что

.

- это матрица, все элементы которой нули, кроме одного :

это номер строки этого места,

- номер столбца.
Задача 3. Найдите

по всем непрерывным дифференцируемым функциям
![$f:[0,1]\rightarrow\mathbb R$ $f:[0,1]\rightarrow\mathbb R$](https://dxdy-04.korotkov.co.uk/f/b/3/4/b3427c0a9db5896bd63abfde6d4544c482.png)
, таким, что

и

.
Задача 4. Пусть

- матрица размера 2 на 2 с рациональными коэффициентами. Пусть существует натуральное

, не равное нулю, такое, что

. Докажите, что либо

, либо

.