IMC 2013

[xmaister]

День 1:
1. Пусть $A,B$- симметрические матрицы, собственные значения которых строго больше единицы. Докажите что собственные значения $AB$ по модулю строго больше 1.
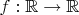
2. Пусть $f: \mathbb{R}\to\mathbb{R}$ дважды дифференцируема и $f(0)=0$. Докажите что существует $x\in(-\pi/2,\pi/2)$, такое что

$$f''(x)=f(x)(1+2\tg^2x)$$

.
3. Пусть $n\ge 2$- натуральное. $2n$ школьников едут на экскурсию по $n$ человек. Найдите наименьшее количество экскурсий, которых необходимо, чтобы каждая пара школьников была на одной экскурсии.
4. Пусть $n\ge 3$, $x_1,\ldots x_n$- неотрицательные действительные числа. Положим что $A=\sum\limits x_i,B=\sum\limits x_i^2, C=\sum\limits x_i^3$. Докажите, что

$$(n+1)Aj^2Bk+(n-2)B^2\ge A^4+(2n-2)AC$$

.
5. Существует ли последовательность комплексных чисел, такая что ряд $\sum\limits_{n=1}^{\infty}a_n^p$ сходится тогда и
только тогда, когда $p$ не простое.

UPD: поправил 2.

[mihailm]

а в 5. $p$ какое?

[xmaister]

Натуральное

[BatMan]

3. 6 увлекательных экскурсий

[xmaister]

BatMan , правильно.

(Оффтоп)

я ее даже ее чита, а оказашась легкая

[mihailm]

xmaister в сообщении #753236 писал(а):

Натуральное

На всякий случай: при $p=1$ сходится, правильно?

[BatMan]

(Оффтоп)

Цитата:

я ее даже ее чита, а оказашась легкая

как всегда

[xmaister]

mihailm
Да

[BatMan]

а если во второй взять косинус?

[arqady]

xmaister в сообщении #753204 писал(а):

4. Пусть $n\ge 3$, $x_1,\ldots x_n$- неотрицательные действительные числа. Положим что $A=\sum\limits x_i,B=\sum\limits x_i^2, C=\sum\limits x_i^3$. Докажите, что

$$(n+1)A^2B+(n-2)B^2\ge A^4+(2n-2)AC$$

.

Пусть $\sum\limits_{i=1}^nx_i=nu$, $\sum\limits_{1\leq i<j\leq n}x_ix_j=\frac{n(n-1)}{2}v^2$ и $\sum\limits_{1\leq i<j<k\leq n}x_ix_jx_k=\frac{n(n-1)(n-2)}{6}w^3$.
Тогда $(n+1)A^2B+(n-2)B^2- A^4-(2n-2)AC=n^2(n-1)^2(n-2)(v^4-uw^3)\geq0$.

[Dave]

xmaister в сообщении #753204 писал(а):

2. Пусть $f: \mathbb{R}\to\mathbb{R}$ дважды дифференцируема. Докажите что существует $x\in(-\pi/2,\pi/2)$, такое что

$$f''(x)=f(x)(1+2\tg^2x)$$

.

Бред какой-то. А если $f(x) \equiv 1-\left(\frac {2x} \pi \right)^2$ ? $f''(x)$ всегда отрицательна, а правая часть положительна в указанном интервале.

[g______d]

1. Из условия следует, что $\|A^{-1}\|,\|B^{-1}\|<1$. Следовательно, $\|(AB)^{-1}\|=\|B^{-1}A^{-1}\|<1$. Обозначим последнюю величину через $m^{-1}$. Таким образом, $\|ABx\|\ge m\|x\|$, где $m>1$.

[sopor]

Во второй задаче есть доп. условие - $f (0)=0$. Пруфлинк - http://mathproblems123.wordpress.com/2013/08/08/imc-2013-problem-2/

[g______d]

А в задаче 1 матрицы вещественные. Для комплексных симметричных я не знаю решения и не уверен, что факт верен.

[xmaister]

День 2:
1. Пусть $ z$-комплексное число. Докажите, что$|z+1|>2\Rightarrow |z^3+1|>1$.
2. Пусть $p,q$-взаимно простые положительные. Докажите, что $\sum\limits_{k=0}^{pq-1}(-1)^{[\frac{k}{p}]+[\frac{k}{q}]}=0$, если $pq$- четно и $1$, если $pq$- нечетно.$ []$- целая часть.
3. Пусть $v_1,\ldots v_d$- единичные векторы в $\mathbb{R}^d$. Докажите, чтобы существует $u$, такой чтобы $\langle u,v_i\rangle\le \frac{1}{\sqrt{d}}$, где $\langle\rangle$- скалярное произведение.
4. Существует ли бесконечное множество натуральных такое чтобы для любых $a ,b$ из этого множества с $a <b$, $a+b$ свободно от квадратов.