Добрый вечер, уважаемые эксперты в области аксиоматической теории множеств! Интересует разрешение нескольких возникших вопросов, которые согласно современные представлениям математиков предъявляют ложные посылы, однако конкретных аксиом ZFC, которые при этом используются неправильно, не удалось найти
Вопрос 1 (Прямой) - О задании действительного числа
Действительное число может быть записано в общем случае, в виде бесконечной непереодической десятичной дроби, при этом верным является любая комбинация десятичных цифр после запятой, за исключением последовательности, в которой начиная с

-ой позиции следует исключительно одни цифры

- она должна быть записана в форме, в которой цифра на

-ой позиции увеличена на единицу, а с

-ой заполнена нулями
В соответствии с таким представлением действительного числа, можно ввести следующую операцию: пусть
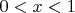
-действительное число, а

- цифра в десятичной записи в

-ой позиции; тогда пусть

представляет собой число, в котором все цифры в десятчной записи вплоть до

-ой позиции совпадают, а на

-ой позиции цифра заменяется по следующему правилу: если

, то

, если

, то

и так далее
В случае если

, то

, и аналогичная операция выполняется для

-ой позиции
Теперь пусть

, применим к нему операцию

и получим новое число, и будем далее выполнять такую же операцию с вновь полученным числом; в таком случае каждое из последующих чисел было получено, в конечном итоге, за счет применения операции

к числу

в количестве

раз
Исходя из предложенной операции, можно сформровать класс эквивалентности между натуральными числами, обозначиющими количество последовательно примененной операции

, и получаемыми бесконечными десятичными дробями, соответствующие действительным числам
Вопрос - какие из аксиом ZFC были нарушены, или же применены неправильно, при рассмотренном построении?Вопрос 2 (Обратный) - О списке действительных чисел
Существует известная теорема, доказывающая невозможность построения биекции между множеством действитльных чисел, в качесве бесконечных десятичных дробей, обладающих свойством из Вопроса 1 относительно заключительных цифр

в описании, и множеством натуральных чисел
Указанная теорема строится на основании предположения, что возможно составить список действительных чисел, в которых каждое из них расположено в своей строке и имеет натуральный номер, что бы означало потенцальную биекцию
Вопрос - какие из аксиом ZFC позволяют обращаться к некоторым строкам из списка, если они не могут иметь натуральных индексов?Здесь можно предпололжть, что речь идет об аксиоме выбора, которая позволяет магическим образом выбрать элемент из бесконечного множества, не имея какого-то описания, как это возможно осуществить
То есть в формальном процессе из указанной теоремы, в отличие от противоречивого интуитивного описания, никакого списка не сущестует: из множества действительных чисел с помощью аксиомы выбора, последовательно производится выбор одного элемента, не равного ни одному из предыдущих выбранных, и этот процесс производится счетное число раз
Вопрос - можно ли сказать, что аксиома выбора постулирует существование random-функции для элементов множеств, позволяя выбирать элементы, не имея ни одного конструктивного критерия, чтобы сделать этоПросьба отвечать исключительно по существу, касательно рассматриваемой аксиоматики; В общем случае всегда можно взять за основу такую собственную аксиоматику, в которой ссылающиеся гипотезы будут верны или не верны