[/quote]
Понятна ваша обеспокоенность отсутствием единого доказательства для всех степеней, но, наверное, и существующее неплохо выглядит с учетом 350 лет мытарства)
Уайлс великий математик,кто тут спорит,да и многие ,кто занимался ВТФ.Просто меня волнуют мелочи,может я не ясно ставлю вопросы,думаю куда проще спрашиваю-почему из уравнения для

и более получена кривая для
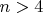
,что тут не понятного,а ответа за три года не нашел.Поэтому и доказательство охватывает все степени ,кроме 3 и 4,а такого не может быть и вы,математики это знаете лучше меня.Вы просто сделали вид,что все хорошо,так сказали великие.Еще есть вопросы,но жду ответа.
-- Чт дек 12, 2013 23:15:34 --Гаджимурат, если вы и дальше будете писать бессвязные эмоциональные сообщения с множеством восклицательных знаков, то вам перестанут отвечать, а может и забанят. Вам это надо?
Если нет, то давайте без эмоций и по порядку.
Сформулируйте один вопрос, на который вам здесь ещё не ответил
С пунктуацией правильно,учту.Вопрос. Если ,в полученной Фреем кривой,

есть числа целые,то есть Ферма не прав,что тогда было бы,кривая имела бы модулярную форму и была бы эллиптической?.Ну не могу я лучше формулировать вопросы.