а можно еще так поставить вопрос. оценить время существования решения задачи
Ну у меня получилось, что на
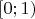
решение единственно (если переписать в виде интегрального уравнения, то отображение будет сжимающим). Тогда оно понятно какое. А дальше оно однозначно восстанавливается по уравнению и тоже единственно (и продолжается до бесконечности).
Вообще достаточно единственности и ограниченности на сколь угодно малом интервале; наверное, это верно с гораздо более общей правой частью.