Тут, КМК, есть небольшая путаница в обозначениях.
Смешана "общая форма" записи регрессии

и "практическая", когда для введения свободного члена не добавляют в матрицу Х столбик из единиц, а рассматривают его отдельно (вычитая средние из X и y, считая коэффициенты, как

, а затем вычисляя его, как

)
Отсюда неясность, откуда взялся
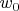
, если его вроде вначале не было.
А сперва надо понять, модель со свободным членом или без него.
Если со свободным - то столбец единиц неявно был в матрице Х, и прогноз имеет вид

, если без свободного - то никакого
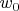
нет.
спасибо, делаю так, то с ответом не сходится никак.
Вот данные.
Код:
x10 =
3.5520 1.5301 3.3059 3.3343 5.0874 20.0835
3.5520 2.2755 2.7097 3.4983 6.0296 20.0835
2.3680 0.8827 1.8968 2.3009 5.2759 20.6337
2.3680 1.1966 2.3846 2.9697 5.6904 22.0093
2.3680 0.9612 2.1678 2.2748 5.4266 21.7342
2.3680 0.9612 1.7884 2.1382 5.4266 21.4590
2.3680 1.3732 2.3846 3.4329 6.5195 21.7342
2.3680 1.1083 2.5742 2.6466 5.2759 19.5332
3.5520 1.9616 2.3846 3.6349 6.4441 22.2844
4.7360 3.4427 4.1459 4.9344 5.0874 19.5332
y10 =
20.0000
18.0000
29.0000
35.0000
35.7000
36.1000
22.3000
25.0000
20.2000
14.0000
вот код в матлабе
Код:
for i=1:6
A1=[x10(:,i).^0, x10(:,i)];
w10(:,i) = ((A1'*A1)^(-1))*(A1'*y10);
end
for i=1:6
w_res(i) = w10(1,i)/w10(2,i);
end
вот что получилось

Код:
w10 =
48.5578 38.1720 47.9864 50.5477 38.0536 -60.3730
-7.7796 -8.0557 -8.7235 -8.0275 -2.2259 4.1085
w_res =
-6.2417 -4.7385 -5.5008 -6.2968 -17.0958 -14.6948
а в ответе стоит
 -- Чт июн 20, 2013 10:15:04 --
-- Чт июн 20, 2013 10:15:04 --если брать без свободного члена, то все равно не сходится с ответом
Код:
for i=1:6
A1=[x10(:,i).^0, x10(:,i)];
w10(:,i) = ((A1'*A1)^(-1))*(A1'*y10);
[b]w_w_10(:,i)=((x10(:,i)'*x10(:,i))^(-1))*(x10(:,i)'*y10);[/b]
end
Код:
w_w_10 =
7.5232 11.6546 8.7635 7.1833 4.4838 1.2276