Что можно сказать о существовании (если существуют, то об асимтотике решений в зависимости от

) решений такого уравнения?
Чтобы было попроще, будем считать

нечётным натуральным числом. Тогда уравнение

можно решать в натуральных числах

,

следующим образом. Положим

,

,

. Тогда

. Поскольку

нечётно, имеем

, откуда

и

. Перебирая тройки

, удовлетворяющие условиям

найдём все решения

. В частности, если

свободно от квадратов, то решений нет. Если

, где
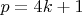
--- простое число, то решений ровно два. Если

, где все

--- простые числа вида

, то решений по крайней мере

штук. В общем случае ответ зависит от арифметических свойств числа

.