В теме "ВТФ для n=3" (
topic60946.html) я дал доказательство с использованием кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Если

, где

,

и

- ненулевые, взаимно-простые целые числа, то

является квадратом целого числа, из чего следует, что
![$x^2-\sqrt[3]{4}(yz)$ $x^2-\sqrt[3]{4}(yz)$](https://dxdy-02.korotkov.co.uk/f/5/2/0/5203ed1029bea38963c4449f3234f45182.png)
является квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
, а дальше, как говорится, дело техники.
В этой теме я предлагаю новое доказательство того, что
![$x^2-\sqrt[3]{4}(yz)$ $x^2-\sqrt[3]{4}(yz)$](https://dxdy-02.korotkov.co.uk/f/5/2/0/5203ed1029bea38963c4449f3234f45182.png)
является квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
, которое не использует единственность разложения на простые множители в этом кольце.
Пусть
(1)

, где

- целое число.
Пусть
(2)
![$x^2-\sqrt[3]{4}(yz)=b^2$ $x^2-\sqrt[3]{4}(yz)=b^2$](https://dxdy-03.korotkov.co.uk/f/6/a/c/6ac07aa2a7e4deec52a190119464f59282.png)
, где

- алгебраическое число.
Из (2) следует:
(3)

.
Из (3) и (1) следует:
(4)

Пусть
(5)

,
где коэффициенты
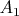
,
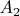
,
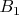
,

- алгебраические числа, обращающие это равенство в тождество, верное при любых значениях

.
Из (5) следует:
(6)

Из (6) следует
(7)

,

и
(8)

,

Из (4) и (5) следует, что один из сомножителей в правой части равенства (5) равен нулю.
Поскольку второй сомножитель получается из первого заменой

на

и
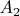
на

, то, без ограничения общности, предположим, что первый сомножитель равен нулю.
То есть:
(9)

Пусть поле
![$F=\mathbb{Q}[A_1]$ $F=\mathbb{Q}[A_1]$](https://dxdy-02.korotkov.co.uk/f/5/3/6/53627470fafe7882f25ebaeaad14c61582.png)
.
Из второго равенства в (8) следует, что

.
Поскольку степень расширения
![$[\mathbb{Q}[b]:\mathbb{Q}]$ $[\mathbb{Q}[b]:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/7/8/3/78380221b343a0d9a324f694824d7e2d82.png)
равна 3 или 6, то степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

или

или

.
Если многочлен (9) относительно

неразложим на множители с коэффициентами из поля

, то степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

или

, иначе степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

.
Покажем, что степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
не равна

.
Предположим обратное, что степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

.
Тогда числа
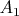
и
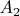
удовлетворяют квадратным уравнениям с целыми коэффициентами, поэтому система уравнений (8) превращается в линейную систему уравнений относительно неизвестных
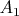
и
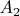
, решением которой являются рациональные числа.
Следовательно, степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

, что противоречит предположению.
Значит если многочлен (9) относительно

неразложим на множители с коэффициентами из поля

, то степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

, иначе степень расширения
![$[F:\mathbb{Q}]$ $[F:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/3/4/8/3489f5b5cf552aad659b1d059dafd2f382.png)
равна

.
В обоих случаях:
(10) степень расширения
![$[\mathbb{Q}[b]:\mathbb{Q}]$ $[\mathbb{Q}[b]:\mathbb{Q}]$](https://dxdy-04.korotkov.co.uk/f/7/8/3/78380221b343a0d9a324f694824d7e2d82.png)
равна

.
Из (2) и (10) следует, что
![$b \in \mathbb{Z}[\sqrt[3]{2}]$ $b \in \mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-04.korotkov.co.uk/f/f/6/1/f6136a409f625d8fa7c34ce9cfee889682.png)
, что и требовалось доказать.