Имеем большую матрицу
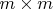
, в строках есть простая закономерность - 1-ца появляется через столбец, потом через 2 (для следующей строки), и т.д.

Можно ли быстро посчитать сумму произвольного столбца, например, для 1-го - 0, для 2-го - 1, для 3-го -1, для 4-го - 2, и т.д?
В голову пришел приблизительно такой алгоритм:
1. Получаем формулу (получил) для

-той строки, до

-того столбца, т.е.

, например

,

,

, и т.д.
2. Получаем формулу

(не могу получить) последней цифры

, например

,

,
 3.
3. Суммируем

до

-ой строки для

-того столбца,

, и надеемся, что эта сумма свернется в функцию без суммы.
Подскажите пожалуйста можно ли получить формулу для пункта
2? Или существует ли другая стратегия решения задачи?