Окрестность точки x

[ex-math]

xmaister
Боюсь, что нет.

[SpBTimes]

xmaister
Оказалось все весьма просто.
Для каких-то двух поворотов исходной дуги на натуральные углы $n_1$ и $n_2$, должны получиться пересекающиеся (в силу конечности длины окружности), но не совпадающие (в силу иррациональности $2 \pi$) дуги. Но тогда, если осуществлять поворот из положения $n_2$ на натуральный угол $n_3 = n_2 - n_1$, мы наложимся на дугу $n_2$ так же, как наложилась $n_2$ на $n_1$. Но еще и остается хвостик (ведь дуги не совпадают). 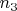Тем самым продолжая поворачивать на все тот же угол $n_3$, за счет этих хвостов можно покрыть всю окружность.