Помогите сделать:
1) Пусть

- группа всех комплексных корней из единицы (т.е. всех таких

, что

для некоторого

). Постройте изоморфизм
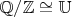
.
2) Изоморфны ли группы

?
3) Найдите все классы сопряженности в группе

.
Я думаю во 2м номере нужно применить теорему о разложении конечно порожденных абелевых групп на циклические и примарные.. Но тогда вопрос, почему по этой теореме нельзя разложить

как

..?