Вы бы хоть формулы привели в порядок, непонятно же ничего. Если Вам нужно написать систему уравнений, можно использовать окружение \begin{cases}первое уравнение\\ второе уравнение\end{cases}. Также правильно расставляйте знаки доллара и теги /math, не заключайте в них ничего лишнего.
После того, как нашли стационарные точки, их нужно исследовать с помощью достаточного условия экстремума. В учебнике формулировка должна быть. Нужно вычислить
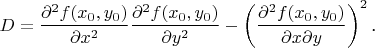
При

и

функция имеет минимум, при

и

- максимум, при

экстремума нет.