Добрый вечер, подскажите, пожалуйста, как тут быть дальше.
Определить область существования и выразить эйлеровы интегралы
1)

Делал так

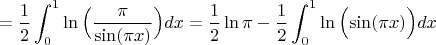
Как взять последний интеграл? Или тут можно сделать иначе?
2)

Тут логарифм сильно смущает, я делал замену

, но ничего хорошего из этого не вышло...