Someone
По Даламберу получился относительно сложный предел:
Wolfram Alpha Это - сложный? Господь с Вами, этот предел относится к числу наипростейших; на самом примитивном уровне (без всяких эквивалентных бесконечно малых и бесконечно больших) нужно просто раскрыть скобки в числителе и знаменателе, а потом разделить числитель и знаменатель на наиболее быстро растущий член.
Mitrius_Math
Вы имеете ввиду, что сравнить, например с

?
Выбор
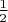
неудачен. Немножко присмотревшись к главным членам в числителе и знаменателе, легко догадаться, какую прогрессию следует выбрать.
Такой же простой, как в признаке Даламбера.
Вот и
Mitrius_Math Вам то же говорит.