Иван_85Прошу прощения, перечитав ваш пост, убедился в том, что сморозил глупость, в своём предыдущем посте.
В своём посте я взял за m - число "людей".
Ну, например, у нас есть 60 человек. То есть

Каждый десятый - математик, следовательно

.
Каждый шестой - шахматист, следовательно
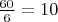
.
Здесь, выходит, шахматистов больше чем математиков. И появились еще некоторые люди без профессии. Как быть в этом случае?
В этом случае, если я не ошибаюсь, шахматистов будет больше, чем математиков в

раз.