Орбиты Жукова

[Pashka]

Сначала проверил, а затем доказал все гипотезы Штейнгарца и теорему Сергея Ворова, которая, кстати, обобщает большую часть этих гипотез.
И всё с помощью проективной геометрии, а именно теоремы обратной к теореме Паскаля.
На самом деле не нужно здесь вводить системы координат, всё оказалось куда проще.

[nnosipov]

Pashka в сообщении #657905 писал(а):

а затем доказал все гипотезы Штейнгарца

Какие именно? Там почти все гипотезы неверны.

[Pashka]

6 точек - основания высот и биссектрис принадлежат орбите Жукова.
6 точек - основания биссектрис и медиан принадлежат орбите Жукова.
6 точек - центры окружностей описанных около 6 треугольников на которые данный треугольник разбивается тремя чевианами (пересекающимися в одной точке) принадлежат орбите Жукова.
6 точек - центры тяжести треугольников на которые разбивается данный треугольник медианами принадлежат орбите Жукова.
Гипотезы о теореме Морлея и орбитах Жукова ещё не смотрел.

-- Чт дек 13, 2012 18:40:08 --

Да, прошу прощения за фразу "все гипотезы". Я имел ввиду те, о которых я помню. Просто статьи на руках нет. Я её пролистал и запомнил основные гипотезы.
При этом некоторые оказались действительно не верными.
Но те, которые я перечислил - верны!

[nnosipov]

Pashka в сообщении #658015 писал(а):

Гипотезы о теореме Морлея и орбитах Жукова ещё не смотрел.

Не тратьте время, они неверны. Лучше попробуйте найти геометрическое доказательство теоремы об инцентре. Вот это было бы интересно.

-- Чт дек 13, 2012 23:01:20 --

Pashka в сообщении #658015 писал(а):

6 точек - центры тяжести треугольников на которые разбивается данный треугольник медианами принадлежат орбите Жукова.

А здесь не окружность ли будет?

[Pashka]

nnosipov в сообщении #658021 писал(а):

Pashka в сообщении #658015 писал(а):

Гипотезы о теореме Морлея и орбитах Жукова ещё не смотрел.

Не тратьте время, они неверны. Лучше попробуйте найти геометрическое доказательство теоремы об инцентре. Вот это было бы интересно.

-- Чт дек 13, 2012 23:01:20 --

Pashka в сообщении #658015 писал(а):

6 точек - центры тяжести треугольников на которые разбивается данный треугольник медианами принадлежат орбите Жукова.

А здесь не окружность ли будет?

В общем случае - нет!

-- Пт дек 14, 2012 16:44:31 --

Кто такой Сергей Воров?

[nnosipov]

Pashka в сообщении #658347 писал(а):

В общем случае - нет!

Это я спутал, надо слово "тяжести" убрать из утверждения, тогда всё в порядке будет. Т.е. центры (а не центры тяжести) этих шести треугольников лежат на одной окружности.

[Alexander Evnin]

В 2000 г. голландец ван Ламун доказал, что центры, окружностей, описанных вокруг треугольников, на которые разбивается треугольник своими медианами, лежат на одной окружности. http://vk.com/kvantik12

-- 23.12.2012, 15:41 --

Об этом написано и в упомянутой выше статье Алексея Мякишева.

[nnosipov]

Alexander Evnin в сообщении #662326 писал(а):

Об этом написано и в упомянутой выше статье Алексея Мякишева.

Да, здесь я этот факт и обнаружил (или в какой-то статье Мякишева в "Forum Geometricorum"). В памяти почему-то отложилось, что эту теорему нашёл Мякишев, а не этот голландец.

[nnosipov]

Ниже приводится доказательство теоремы об инцентрах и её обобщения. Символ $l(P,v)$ обозначает прямую, проходящую через точку $P$ в направлении вектора $v$.

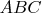
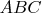
Пусть $ABC$ --- треугольник с углами $\alpha$,$\beta$, $\gamma$, $AA_1$,$BB_1$, $CC_1$ --- его биссектрисы, $I$ --- их точка пересечения (инцентр треугольника $ABC$), $P_1$, $P_2$, $P_3$, $P_4$, $P_5$, $P_6$ --- инцентры треугольников $AB_1I$, $A_1BI$, $BC_1I$, $B_1CI$, $CA_1I$, $C_1AI$ соответственно. Будем считать, что треугольник расположен на комплексной плоскости так, что $A=0$, $B=1$ (вещественную ось представим горизонтальной и идущей слева направо, мнимую ось --- направленной вертикально вверх, точку $C$ --- лежащей в верхней полуплоскости). Положим

$$ a=\cos{\frac{\alpha}{4}}+i\sin{\frac{\alpha}{4}}=z_1, \quad b=\cos{\frac{\beta}{4}}+i\sin{\frac{\beta}{4}}=z_2, \quad c=\cos{\frac{\gamma}{4}}+i\sin{\frac{\gamma}{4}}=\frac{\zeta}{z_1z_2},$$

где $\zeta=\cos{45^\circ}+i\sin{45^\circ}$. Точку $C$ можно получить как точку пересечения прямых $l(A,a^4)$ и $l(B,b^{-4})$, а точку $I$ --- как точку пересечения прямых $l(A,a^2)$ и $l(B,b^{-2})$:

$$ C=\frac{z_1^8(z_2^8-1)}{z_1^8z_2^8-1}, \quad I=\frac{z_1^4(z_2^4-1)}{z_1^4z_2^4-1}. $$

Далее рассмотрим, например, треугольник $AB_1I$. Как нетрудно увидеть,

$$ \angle IAB_1=\frac{\alpha}{2}, \quad \angle AIB_1=\frac{\alpha+\beta}{2}. $$

Значит, инцентр $P_1$ треугольника $AB_1I$ можно вычислить как точку пересечения прямых $l(A,(I-A)a)$ и $l(I,(A-I)a^{-1}b^{-1})$:

$$ P_1=\frac{z_1^6(z_2^4-1)} {(z_1^4z_2^2-1)(z_1^2z_2^2+1)}. $$

Аналогично, инцентр $P_2$ треугольника $A_1BI$ --- это точка пересечения прямых $l(B,(I-B)b^{-1})$ и $l(I,(B-I)ab)$:

$$ P_2=\frac{z_1^2(z_2^2-1)(z_1^2z_2^4+z_1^2z_2^2+z_1^2+z_2^2)} {(z_1^2z_2^4-1)(z_1^2z_2^2+1)}. $$

Остальные инцентры вычисляются из аналогичных соображений. Так, например, имеем

$$ P_3=\frac{z_1^2(z_2^2-1)(z_1^4z_2^2-\zeta^2z_1^2z_2^4-\zeta^2z_1^2z_2^2+1)} {(z_1^4z_2^4-1)(z_1^2-\zeta^2z_2^2)}. $$

Инцентр $P_3$ получен как точка пересечения прямых $l(B,b^{-1})$ и $l(I,(B-I)b^{-1}c^{-1})$, поэтому здесь впервые появилось число $\zeta$. В выражениях для инцентров $P_4$, $P_5$, $P_6$, которые не приводятся, оно также будет.

В комплексных координатах $(z,\overline{z})$ кривая 2-го порядка описывается уравнением

$$ Kz^2+Lz\overline{z}+M\overline{z}^2+Uz+V\overline{z}+W=0. $$

Очевидно, существование нетривиального набора коэффициентов $K$, $L$, ..., $W$, для которого будут выполнены равенства

$$ KP_j^2+LP_j\overline{P_j}+M\overline{P_j}^2+UP_j+V\overline{P_j}+W=0, \quad j=1,\,2,\,\dots,\,6, $$

равносильно тому, что определитель

$$ \Delta=\Delta(P_1,\ldots,P_6)= \det{([P_j^2,P_j\overline{P_j},\overline{P_j}^2,P_j,\overline{P_j},1]_{j=1}^6)} \eqno(*) $$

равен нулю. Выражение для $P_j$ имеет простую структуру --- это рациональная дробь от $z_1$, $z_2$ и $\zeta$. Поэтому вычисление определителя $\Delta$ не может быть проблемой. Если учесть соотношение $\zeta^4+1=0$, то чудесным образом получим $\Delta=0$.

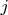
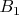
Эту теорему можно обобщить, рассматривая дополнительно все центры окружностей, вневписанных в треугольники $AB_1I$, $A_1BI$, $BC_1I$, $B_1CI$, $CA_1I$, $C_1AI$. Обозначим через $P_j^X$ центр вневписанной в $j$-й треугольник окружности, лежащий против вершины $X$ (так, например, $P_4^{B_1}$ --- это центр вневписанной в треугольник $B_1CI$ окружности, который расположен против вершины $B_1$). Точнее, нас будут интересовать шестёрки точек $(Q_1,\ldots,Q_6)$, где $Q_j$ --- это либо инцентр $P_j$, либо один из центров $P_j^X$. Имеем $4^6$ таких шестёрок, одна из которых, а именно, $(P_1,\ldots,P_6)$, обладает тем свойством, что её точки принадлежат одной кривой 2-го порядка (эллипсу в данном случае). Особенность представленного выше доказательства в том, что автоматически можно предъявить ещё одну шестёрку точек, для которой это также будет верно. Таковой является $(P_1,P_2,P_3^{B},P_4^{B_1},P_5^{A_1},P_6^{A})$ (но её точки уже лежат не на эллипсе, а на гиперболе). Это потому, что можно взять $\zeta=\cos{135^\circ}+i\sin{135^\circ}$, и равенство $\zeta^4+1=0$ по-прежнему будет иметь место. Далее, хотя бы из спортивного интереса, можно отыскать все шестёрки $(Q_1,\dots,Q_6)$ с этим свойством. Поскольку выражения для центров $P_j^X$ ничем принципиально не отличаются от выражений для инцентров $P_j$, вычисление любого из определителей $\Delta(Q_1,\ldots,Q_6)$ будет не сложнее, чем вычисление определителя $(*)$. Включаем компьютер, и через некоторое время находим ровно $32$ шестёрки, для которых $\Delta(Q_1,\ldots,Q_6)=0$. Вот некоторые примеры: $(P_1,P_2,P_3,P_4,P_5^{I},P_6^{I})$, $(P_1,P_2,P_3^{I},P_4^{I},P_5^{I},P_6^{I})$, $(P_1,P_2,P_3^{B},P_4^{B_1},P_5^{C},P_6^{C_1})$, $(P_1^{I},P_2^{I},P_3^{B},P_4^{B_1},P_5^{C},P_6^{C_1})$, $(P_1^{I},P_2^{I},P_3^{B},P_4^{B_1},P_5^{A_1},P_6^{A})$, $(P_1^{I},P_2^{I},P_3^{I},P_4^{I},P_5^{I},P_6^{I})$. Встречаются и эллипсы, и гиперболы.

[nnosipov]

nnosipov в сообщении #658021 писал(а):

Не тратьте время, они неверны.

А вот здесь я оказался неправ. Как выяснилось, осенью, когда проверял гипотезы, относящиеся к рис. 18 и 19 (см. статью Штейнгарца или прилагаемый файл), в обоих случаях неправильно ввёл в программу значение соответствующей константы $\zeta$. Сейчас решил перепроверить --- и всё сошлось, т.е. соответствующий определитель $\Delta$ действительно равен нулю. Однако гипотеза, относящаяся к рис. 20, всё же неверна.

[Alexander Evnin]

Продолжение темы - в новой статье А.Г.Мякишева http://geometry.ru/persons/myakishev/papers/conj.pdf

[nnosipov]

С точки зрения символьных вычислений применение теоремы, обратной к теореме Паскаля, приводит к такому же выражению, что и раскрытие определителя $\Delta$. Поэтому вычислительное доказательство Мякишева теоремы об инцентрах мне представляется только логически более сложным. Оно не содержит ни новых идей, ни обобщений.